DragAnything: Motion Control for Anything using Entity Representation
研究背景与问题
目的
基于轨迹的可控视频生成。
现有方法对比及局限性
| 方法 | 核心思想 | 局限性 |
|---|---|---|
| DragNUWA [48] | 稀疏轨迹→密集流空间 | 依赖单点,无法表征复杂物体运动 |
| MotionCtrl [42] | 轨迹坐标→矢量图 | 单点控制,忽略物体内部结构 |
| DragAnything | 实体表示→多属性控制 | 解决单点表征不足的问题 |
传统方法(如DragNUWA)通过单点轨迹控制像素区域,存在以下问题:
- 无法区分物体与背景,导致控制歧义。
在DragNUWA生成的视频中,拖动云朵的某个像素点并未导致云朵移动,反而引发了摄像头向上运动。这表明模型无法感知用户意图(控制云朵),说明单点轨迹无法表征实体。
- 轨迹点表示范式下,靠近拖动点的像素受更大影响。
DragNUWA生成视频中,靠近拖动点的像素运动幅度更大,而用户期望的是物体整体按轨迹运动,而非局部像素变形。
本文核心贡献
- 通过使用实体表示(entity representation)来实现可控视频生成中对任意物体的运动控制。
- 实体表示是一种开放域嵌入,能够表示任何对象(包括背景),从而实现对多样化实体的运动控制。
- 允许对多个对象进行同时且独立的运动控制。
主要方法
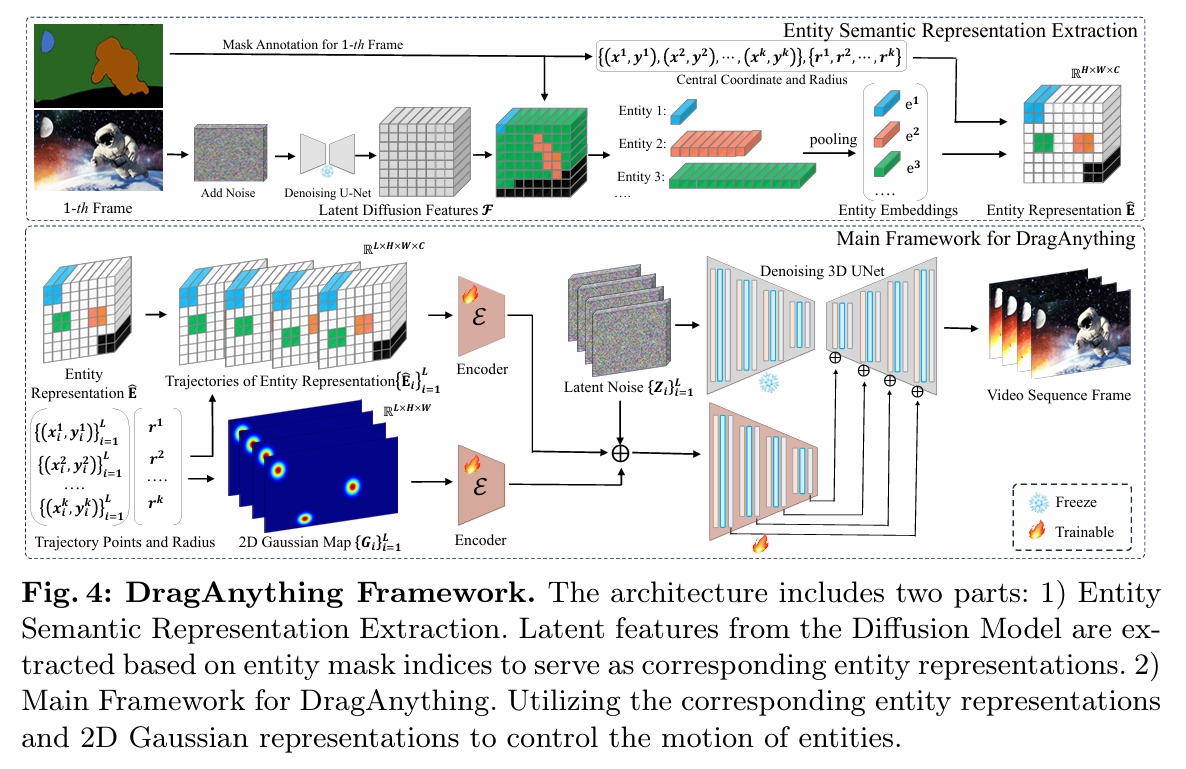
该架构包含两部分:
- 实体语义表示提取:基于扩散模型的潜在特征,通过实体掩码的坐标索引提取对应特征,作为实体的语义表示。
- DragAnything主框架:SVD
实体语义表示提取
| 步骤 | 输入 | 输出 | 方法描述 |
|---|---|---|---|
| 1. 扩散逆过程提取潜在噪声 | 首帧图像 \( I \in \mathbb{R}^{H \times W \times 3} \),实体掩码 \( M \in {0,1}^{H \times W} \) | 潜在噪声 \( \bm{x}_t \in \mathbb{R}^{H \times W \times 3} \) | 基于固定马尔可夫链逐步向图像添加高斯噪声(扩散前向过程),生成潜在噪声 \( \bm{x}_t \)。公式:\( \bm{x}_t = \sqrt{\alpha_t} I + \sqrt{1-\alpha_t} \epsilon \)。 |
| 2. 提取潜在扩散特征 | 潜在噪声 \( \bm{x}_t \),时间步 \( t \) | 潜在扩散特征 \( \mathcal{F} \in \mathbb{R}^{H \times W \times C} \) | 使用预训练去噪U-Net \( \epsilon_\theta \) 单步前向传播提取特征:\( \mathcal{F} = \epsilon_\theta(\bm{x}_t, t) \)。 |
| 3. 实体嵌入提取与池化 | 潜在扩散特征 \( \mathcal{F} \),实体掩码 \( M \) | 池化后的实体嵌入 \( {e_1, e_2, \ldots, e_k} \in \mathbb{R}^{C} \) | 根据掩码 \( M \) 的坐标索引提取特征向量,通过平均池化生成紧凑的实体嵌入。公式:\( e_k = \frac{1}{N} \sum_{i=1}^N f_i \)。 |
| 4. 嵌入与轨迹点关联 | 实体嵌入 \( {e_k} \),首帧实体中心坐标 \( {(x_k, y_k)} \) | 最终实体表示 \( \hat{E} \in \mathbb{R}^{H \times W \times C} \) | 初始化零矩阵 \( E \),将实体嵌入插入对应轨迹中心坐标位置(如图5所示),生成时空对齐的实体表示 \( \hat{E} \)。 |
二维高斯表示提取
目的:靠近实体中心的像素通常更为重要。希望实体表示更聚焦于中心区域,同时降低边缘像素的权重。
| 步骤 | 输入 | 输出 | 方法描述 |
|---|---|---|---|
| 1. 轨迹点与参数输入 | 轨迹点序列:{ {\((x _ i ^ 1, y _ i ^ 1)\)}\( _ {i=1} ^ L, \ldots, \){\((x _ i ^ k, y _ i^k)\)}\( _ {i=1}^L \) } 半径参数:\({r_ 1, \ldots, r_ k}\) | 原始轨迹点及控制范围的参数 | 输入用户提供的轨迹点序列(每个实体\(k\)对应\(L\)个轨迹点)及半径参数\(r_k\)(决定高斯分布范围)。 |
| 2. 高斯热图生成 | 轨迹点\((x_i^k, y_i^k)\),半径\(r_k\) | 二维高斯热图序列 \({G_i}_{i=1}^L \in \mathbb{R}^{H \times W}\) | 为每个轨迹点生成高斯分布热图,公式: \(G_i(h,w) = \exp\left(-\frac{(h - x_i^k)^2 + (w - y_i^k)^2}{2\sigma^2}\right)\),其中\(\sigma = r_k\),中心权重最大,边缘衰减。 |
| 3. 高斯特征编码 | 高斯热图序列 \({G_i}\) | 编码后的高斯特征 \(E({G_i}) \in \mathbb{R}^{H \times W \times C}\) | 通过编码器\(E\)(如3D U-Net)对高斯热图进行时空编码,提取与运动相关的条件特征。 |
| 4. 特征融合 | 编码后的高斯特征 \(E({G_i})\),实体表示 \(\hat{E}\)(来自3.3节) | 融合后的增强实体表示\(\hat{E}_{\text{fused}} \in \mathbb{R}^{H \times W \times 2C}\) | 将高斯特征与实体表示通过通道拼接或跨注意力机制融合,增强模型对中心区域的关注。 |
训练
基模型:Stable Video Diffusion(SVD)
优化器:AdamW
客观评估指标:
- 视频质量评估:FID、FVD
- 物体运动控制性能评估:通过预测轨迹与真实轨迹的欧氏距离(ObjMC)量化运动控制精度。
数据集:VIPSeg
实验

结论:SOTA