POMP: Physics-constrainable Motion Generative Model through Phase Manifolds

大量关于实时运动生成的研究主要聚焦于运动学层面，这常常导致物理上失真的结果。在本文中，我们提出了POMP("Physics-consistent Human Motion Prior through Phase Manifolds"，即"通过相流形实现物理一致的人体运动先验")，这是一个新颖的、基于运动学的框架。它利用相流形来对齐运动先验与物理约束，从而合成物理一致的运动。

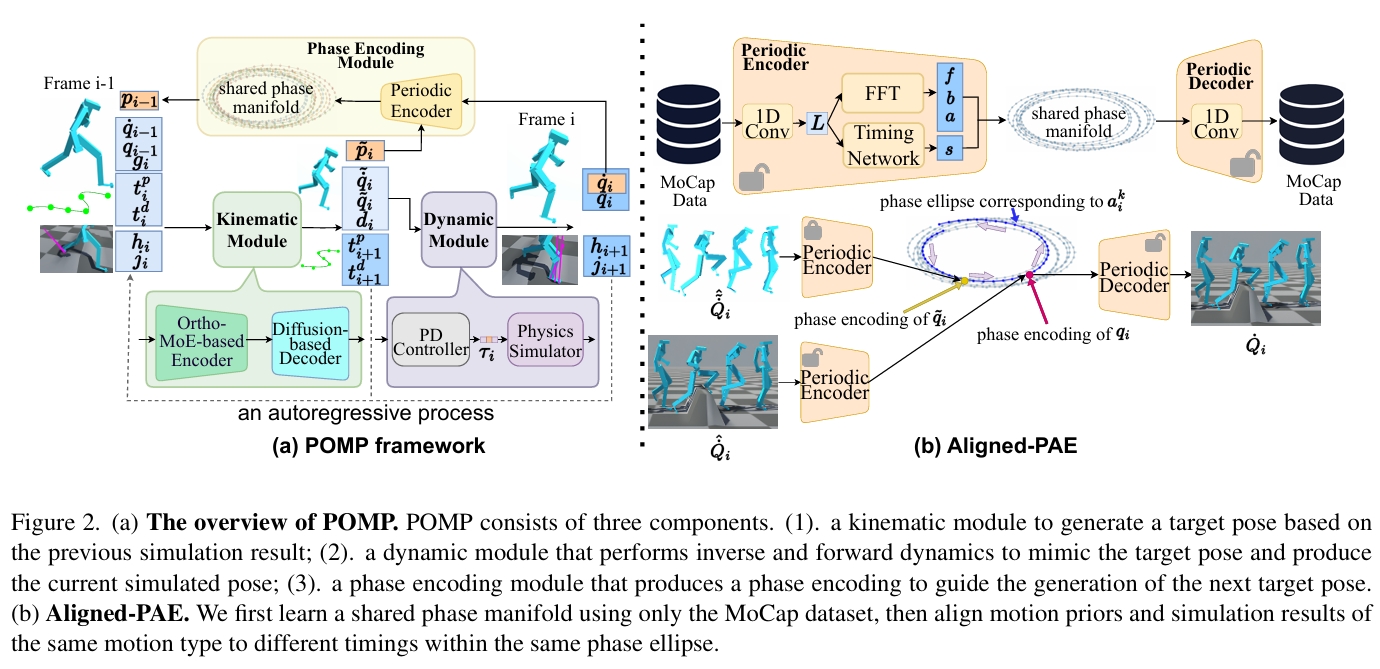
POMP作为一个逐帧的自回归模型运行，包含三个核心组件：一个基于扩散的运动学模块、一个基于仿真的动力学模块和一个相位编码模块。在每一时间步，运动学模块先生成一个初始目标姿态，随后该姿态由动力学模块进行优化(通过模拟人-环境交互)。虽然物理仿真确保了遵循物理定律，但它可能会损害姿态的运动学合理性。因此，直接将仿真结果用于后续帧预测可能会导致误差累积。

为了解决这个问题，相位编码模块在相流形中进行语义对齐。此外，我们提出了一套在Unity引擎中实现的流程，用于生成地形图并从现有的运动捕捉(MoCap)数据中提取全身运动冲量。所收集的地形拓扑和运动冲量数据促进了POMP的训练，使其能够稳健地响应基础接触力和施加的动力学。

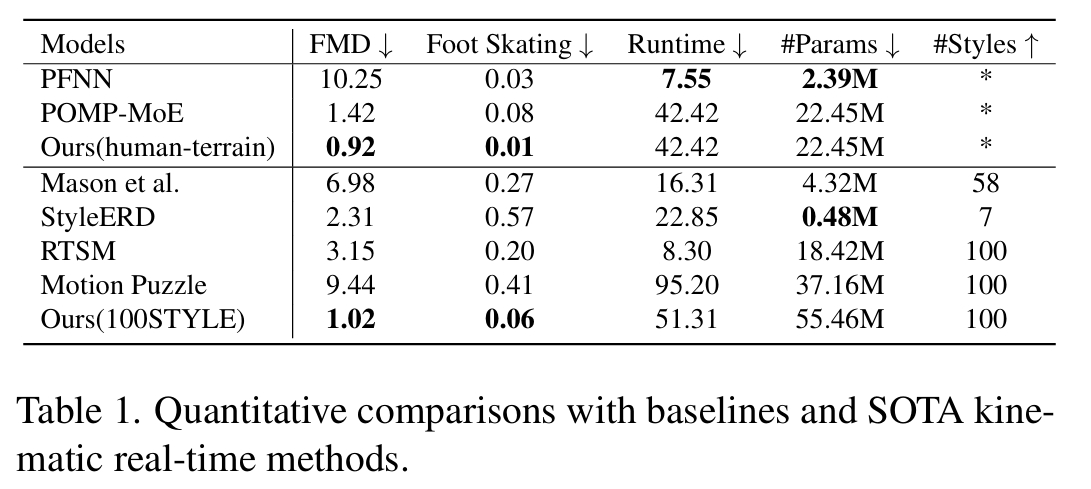
广泛的评估表明，POMP在各种情境、地形和物理交互中均表现出色。

研究背景与问题

要解决的问题

物理合理的实时运动生成

本文方法

这是一个基于运动学的框架，它利用相流形将运动先验与物理约束对齐，从而合成物理上真实的运动。
POMP 作为一个逐帧的自回归模型运行，包含三个核心组件：一个基于扩散的运动学模块、一个基于仿真的动力学模块和一个相位编码模块。在每个时间步，

运动学模块：通过学到的运动先验生成一个目标姿态；
动力学模块：强制执行动态约束并产生一个仿真姿态(不可微)；
相位编码模块：将仿真姿态投影回运动先验，并获取其相位位置编码。
这些处理后的状态向量递归地输入后续的姿态生成。

因为仿真步骤会引起的运动学畸变，累积的误差可能使结果偏离运动学模块学习到的运动先验，导致后续运动生成失败。为了解决这个问题，相位编码模块在相流形中应用语义对齐，将仿真结果投影回运动先验。

本文优势

它将计算密集型的动力学模块置于基于梯度的训练循环之外，从而降低了计算复杂度。
它在相流形中进行语义对齐，从而解决了领域鸿沟问题。
它允许更广泛的应用，能够实现准物理效果，而无需特定于模拟器的专业知识。

主要贡献

一种新颖的基于运动学的生成模型，能够实时对物理扰动进行主动和被动响应。
首次采用基于相位的语义对齐方法来解决运动学运动先验与仿真姿态之间的领域鸿沟。
开发了一个流程，用于从动捕数据集中进行地形重建和全身运动冲量提取。

主要方法

[TODO] 图2

运动表示

第 i 帧的运动变量 (motion variables) xi 由四部分组成：角色状态、环境信息、相位变量和轨迹位置。

角色状态

身体关节的位置
身体关节的速度
根关节（通常指骨盆或臀部在 x-z 平面上的速度
根关节绕 y 轴的旋转角速度
独热编码步态向量，指示角色的步态类型（例如：站立、行走、慢跑、蹲下、跳跃、撞击、躺下、起身）。

环境信息

周围地形高度
全身接触冲量

相位变量

整个时间窗口上的相位编码
时间窗口未来一半的输出相位变量

相位编码由 aligned-PAE 模块生成（或提取）

轨迹位置

用户控制的整个时间窗口的轨迹位置投影到 2D x-z 平面上表示
用户控制的整个时间窗口的方向投影到 2D x-z 平面上表示
预测的轨迹变量的轨迹位置投影到 2D x-z 平面上表示
预测的轨迹变量的方向投影到 2D x-z 平面上表示

运动学模块

OrthoMoE-based Encoder

xi：包含运动表示中的全部输入信息，共541维
wk：1024维

输入	输出	方法
xi中的相位变量	混合系数a	门控网络Eg
xi	相位编码wk	Em中的八个专家网络
相位编码	每个专家对应的相位编码和混合系数	加权求各

约束：各个专家网络的输出互相正交

Diffusion based Decoder

w:条件，1024W
zi:输出，包含xi中h,j以外的信息，8 * 388维

yi = ∑^8_{k=1} α_k z_k

为了在不牺牲质量的前提下加速逆向过程，从 Analytic-DPM 获得灵感，将方程 (3) 中的协方差项\( λ^2_{τ_n} I \) 替换为一个解析估计

动力学模块

逆动力学 (控制)

使用比例微分（PD）控制器，根据运动学模块提供的目标姿态和角色的当前状态(姿态和速度)，计算所需的关节力/扭矩 τ

前向动力学 (仿真)

物理引擎接收 τ 和当前状态，结合环境力（如重力、接触力、碰撞力），计算角色的瞬时加速度。

计算出的加速度用于更新运动状态(姿态和速度)

相位编码模块

动力学模块生成的物理上合理的姿态可能落在运动学运动先验之外，导致在基于 qi 生成下一个目标姿态 q^{i+1} 时破坏运动的连续性。

周期性自编码器 = Periodic Autoencoder = PAE，负责从运动数据中学习一个紧凑的相流形表示。

输入	输出	方法
纯净的 MoCap 数据	运动学速度序列，维度：T * 3NJ
速度序列，维度：T * 3NJ T=121	低维的latent embedding，维度：T * 5 5 对应流形的五个通道假设每个通道 (t=0..4) 都可以近似看作一个正弦波。	1D 卷积层 1D Conv 擅长捕捉时间序列中的局部模式和特征。
低维的latent embedding，维度：T * 5	a_i：振幅 f_i：频率 b_i：偏移	可微FFT层
低维的latent embedding，维度：T * 5	s_i：相移	使用一个 MLP单独预测
a_i, f_i, b_i, s_i	重构的latent embedding	Li = ai · sin(2π · (fi · T - si)) + bi
重构的latent embedding	速度曲线	1D 反卷积层
输入的速度序列输出的速度序列	Loss	MSE

训练完成后，相位编码pei ∈ R^{10} 通过以下方式计算：
pei(2t) = a_i^{(t)} · cos(2π · s_i^{(t)})
pei(2t+1) = a_i^{(t)} · sin(2π · s_i^{(t)})
其中 t 是通道索引 (channel index)（t = 0, 1, 2, 3, 4）。

pe ∈ 2×C×T，C=5，T=0.5L+1=7
{f, a, b} ∈ 3×C×T

用于计算重建的速度序列

输入给 PAE 的速度序列的数据由三部分组成：

过去 (i-60:i)：使用真实仿真速度。
近期未来 (i+1:i+20)：使用人工仿真速度。
较远未来 (i+21:i+60)：使用目标速度。

人工仿真速度是指基于前面的物理仿真的加速度计算得到的速度。

实验

[TODO] 表1

ReadPapers