向量

全篇以2D为例，但对高维同样适用。

向量性质 [07：54]

方向: $ B - A $ 或 $ \vec{a} $
长度：$ ||B-A || $ 或 $ ||\vec{a}|| $ (与起点无关)
单位向量：$ \vec{a}=\frac{\vec{a}}{||\vec{a}||} $，模长为1，通常用于表示方向

向量一般默认为列向量，所以书写公式时，一个向量写为 $\vec{a}=\left( x, y \right) ^T$，其长度为$||\vec{a}|| = \sqrt{x^2 + y^2}$

向量加法

代数意义

$$ \vec{a}=\left( x_1, y_1 \right) ^T , \vec{b}=\left( x_2, y_2 \right) ^T $$

$$ \vec{a}+\vec{b}=\left( x_1+x_2, y_1+y_2 \right) ^T $$

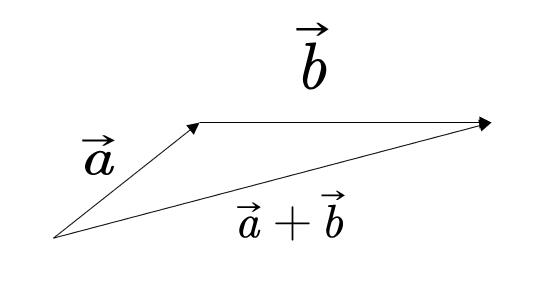
向量点乘

几何意义

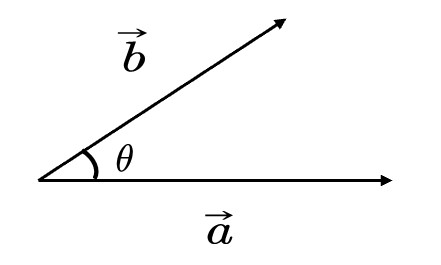
$$ \vec{a}\cdot \vec{b}=||\vec{a}||\cdot ||\vec{b}||\cdot \cos <\vec{a}, \vec{b}> $$

向量点乘的结果是标量

📌补充： 由 $ \vec{a} $ 到 $ \vec{b} $ 的夹角 $ <\vec{a},\vec{b}> $ 是 $ \theta $ , 如果是由 $ \vec{b} $ 到 $ \vec{a} $ 的夹角 $ <\vec{b}, \vec{a}> $ , 则为 $ -\theta $ 。由于cos是关于x轴对称的，因此$a \dot b = b \dot a$

代数意义

$$ \vec{a}=\left( x_1, y_1 \right) ^T , \vec{b}=\left( x_2, y_2 \right) ^T $$

$$ \vec{a}\cdot \vec{b}=x_1x_2+y_1y_2 $$

性质

交换律：$ \vec{a}\cdot \vec{b}=\vec{b}\cdot \vec{a} $
分配律： $ \vec{a}\cdot(\vec{b}+\vec{c})=\vec{a}\cdot \vec{b}+\vec{a}\cdot \vec{c} $
结合律： $ (k\cdot \vec{a})\cdot \vec{b}=\vec{a}\cdot (k\cdot \vec{b})=k\cdot(\vec{a}\cdot \vec{b}) $

作用

计算两个向量之间的夹角

$ \cos \theta =\frac{\vec{a}\cdot \vec{b}}{||\vec{a}||\cdot ||\vec{b}||} $

当a和b都是单位向量时，可简化为：

$$ \cos \theta = \vec{a}\cdot \vec{b} $$

计算一个向量投影在另一个向量上的投影

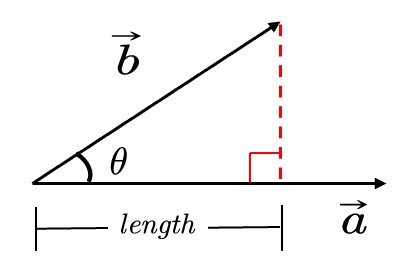
b在a的投影为$\vec{b}_{\bot}$，其长度为：

$$ length=||\vec{b}||\cos \theta =||\vec{b}||\frac{\vec{a}\cdot \vec{b}}{||\vec{b}||\cdot ||\vec{a}||}=\frac{\vec{a}}{||\vec{a}||}\vec{b}=\hat{a}\cdot \vec{b} $$

其方向同a。

因此：

$$ \vec{b}_{\bot} = (\hat{a}\cdot \vec{b}) \hat a $$

把向量分解成垂直和平行的两个向量
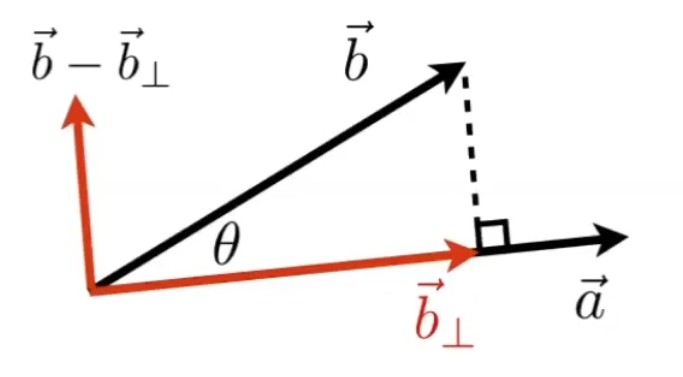
计算两个向量有多接近

两个向量做点乘，可以反映二者方向的“接近”程度

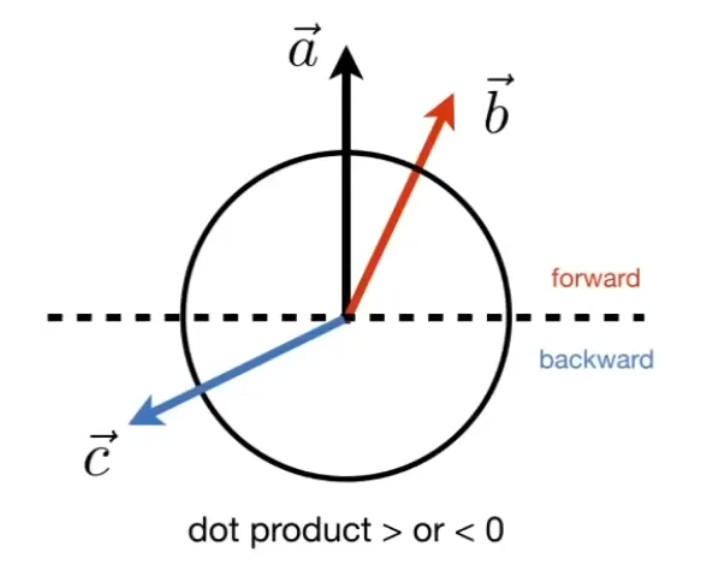
表示方向是否相同：我们假设 $ \vec{a} $ 已给定，如果一个向量的终点落在虚线上半部分，例如 $ \vec{b} $ ，则可以认为该向量在方向上与 $ \vec{a} $ 是相同的或是说都是向前的，此时$\hat a \cdot \hat b > 0$；如果一个向量，例如 $ \vec{c}$，终点落在虚线下半部分，则可以认为 $ \vec{a} $ 和 $ \vec{c}$ 两个向量的方向基本是相反的，此时$\hat a \cdot \hat b < 0$

表示接近程度：点乘结果落在 $[-1, 1]$ 上，数值越大越接近，结果为1时方向相同。数值越小方向越远，为-1时方向正好相反。

📌补充：（点乘： $ \vec{a}\cdot \vec{b} > 0 $ ，方向相同； $ \vec{a}\cdot \vec{c} < 0 $ ，方向相反）

向量叉乘

几何意义

$ \vec{c}=\vec{a}\times \vec{b} $

$\vec{c}$ 是一个向量，方向同时与 $\vec{a}$ 和 $\vec{b}$ 垂直（右手法则），大小为 $||\vec{a}||\cdot ||\vec{b}||\cdot \sin \theta $ ($\theta$ 是a到b的夹角)

✅右手螺旋法则：

$\vec{c}=\vec{a}\times \vec{b}$

右手手指指向 $\vec{a}$ 方向，然后沿着去往 $\vec{b}$ 的方向握紧四指，此时大拇指指向的方向，就是 $\vec{c}$ 的方向。

$\sin \theta = -\sin(-\theta)$，因此$a\times b = b\times a$

性质

[34：15]

$ \vec{x}\times \vec{y}=+\vec{z} $
$ \vec{y}\times \vec{x}=-\vec{z} $
$ \vec{y}\times \vec{z}=+\vec{x} $
$ \vec{z}\times \vec{y}=-\vec{x} $
$ \vec{z}\times \vec{x}=+\vec{y} $
$ \vec{x}\times \vec{z}=-\vec{y} $
$ \vec{a}\times \vec{b}=-\vec{b}\times \vec{a} $ (不满足交换律)
$ \vec{a}\times \vec{a}=\vec{0} $ （不是0，而是长度为0的向量）
$ \vec{a}\times \left( \vec{b}+\vec{c} \right) =\vec{a}\times \vec{b}+\vec{a}\times \vec{c} $ （分配律）
$ \vec{a}\times \left( k\vec{b} \right) =k\left( \vec{a}\times \vec{b} \right) $ （结合律）

左手则符号相反

📌 在一个三维坐标系中，如果$ \vec{x}\times \vec{y}=\vec{z}$，那么这个坐标系称为右手坐标系。

\[ \vec{a}\times \vec{b}=\left( \begin{array}{c} y_az_b-y_bz_a\\ z_ax_b-x_az_b\\ x_ay_b-y_ax_b \end{array} \right) = \left[ \begin{matrix} 0& -z_a& y_a\\ z_a& 0& -x_a\\ -y_a& x_a& 0\\ \end{matrix} \right] \left[ \begin{matrix} x_b\\ y_b\\ z_b\\ \end{matrix} \right] \]

💡思考： 这个式子中，$ x_a,y_a,z_a $ 是$ \vec{a}$ 在三维坐标系中的三个坐标分量的代数表示。叉乘只用于3D中，在2D中没有定义。

式子中的矩阵称为dual matrix of a，常写作$A^*$

❗ 在本课程中默认使用右手坐标系，OPENGL, UE, unity等api默认使用左手坐标系。

在图形学中的作用

判定左和右

📌左右： 目标向量逆时针旋转指向的区域，是目标向量的左侧，反之是右侧。

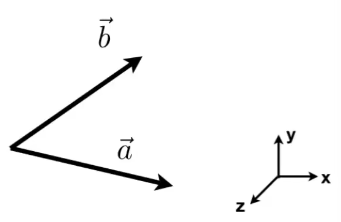
如果$ \vec{a}\times \vec{b} $ 的结果是正值，即与 $Z$ 轴方向相同，就表示 $\vec{b}$ 在 $\vec{a}$ 的左侧。

❓ 叉乘的结果是一个向量，向量没有正负属性，什么叫结果是正的？
答：这里假设a和b都是xy平面上的向量，即
$$ a^\top = (x_a, y_a, 0) \\ b^\top = (x_b, y_b, 0) $$ $c = a \times b$，那么
$$ c^\top = (0, 0, z_c) $$ 在这种情况下，$z_c > 0$认为结果是正的，b在a的左侧。
离开了前面的假设，就不能用这种方法简单的判断了。

判断内和外

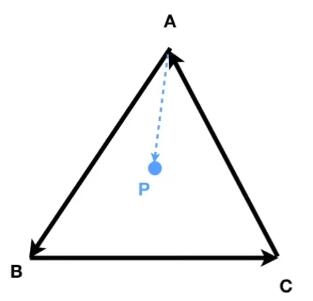
✅如何判断P点在A、B、C的内部？

$ AB\times AP $，可以得到 $AP$ 在 $AB$ 的左侧。$ BC\times BP $，可以得到 $BP$ 在 $BC$ 的左侧。$ CA\times CP $，可以得到 $CP$ 在 $CA$ 的左侧。这样，就可以判断出P点在A、B、C的内部（P点在这三条边的同一侧）。
构建右手坐标系

有三个单位向量，两两垂直：

$||\vec{u}||=||\vec{v}||=||\vec{w}||=1$

$\vec{u}\cdot \vec{v}=\vec{v}\cdot \vec{w}=\vec{u}\cdot \vec{w}=0$

且 $\vec{w}=\vec{u}\times \vec{v}$

则这三个向量构成一个右手坐标系。

可以把任意一个向量分解到轴上去：

$\vec{p}=\left( \vec{p}\cdot \vec{u} \right) \vec{u}+\left( \vec{p}\cdot \vec{v} \right) \vec{v}+\left( \vec{p}\cdot \vec{w} \right) \vec{w}$
- $\left( \vec{p}\cdot \vec{u} \right)$ 是投影长度
- $\vec{u}$ 是方向

本文出自CaterpillarStudyGroup，转载请注明出处。
https://caterpillarstudygroup.github.io/GAMES101_mdbook/