正交投影

准备工作
把相机 view 变换为期望 view(转换到原点),方法是让相机参数乘以一个矩阵。
为了保持camera和object的相对位置不变,object也要同样乘以这样一个矩阵。
这样调整之后,object位于z轴负方向上的某个位置。
正交投影的主要过程
$$ M_{ortho} = M_{scale} \cdot M_{trans} $$
💡 PPT 介绍了正交投影的一种简单理解的方式,让人能够直观地理解正交投影的结果,却也引入的歧义。让人误以为正交投影就是这么简单的过程。以至于后面讲正交投影的完整过程时听众会觉得confuse,为什么会有两个不一样的正交投影流程?因此在本文是中去掉了第一种理解方式。
正交投影中的平移

| 当前位置 | 期望位置 | |
|---|---|---|
| 左右 | [l,r] | [-(r-l)/2, (r-l)/2] |
| 上下 | [b,t] | [-(t-b)/2, (t-b)/2] |
| 远近 | [f,n] | [-(n-f)/2, (n-f)/2] |
📌补充: 由于投影的设定,l在坐标值上,小于r;b小于t,f小于n(因为朝向-Z轴)
正交投影的平移矩阵为:
\[ M_{trans}=\left[ \begin{matrix} 1& 0& 0& -\frac{r+l}{2}\\ 0& 1& 0& -\frac{t+b}{2}\\ 0& 0& 1& -\frac{n+f}{2}\\ 0& 0& 0& 1\\ \end{matrix} \right] \]
正交投影中的缩放
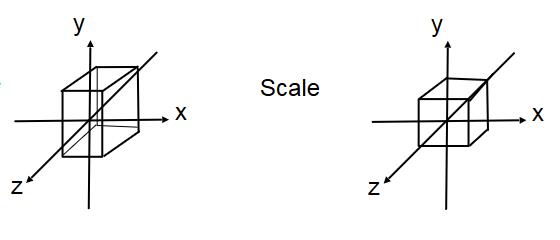
与平移同理。
正交投影的缩放矩阵为:
\[ M_{scale}=\left[ \begin{matrix} \frac{2}{r-l}& 0& 0& 0\\ 0& \frac{2}{t-b}& 0& 0\\ 0& 0& \frac{2}{n-f}& 0\\ 0& 0& 0& 1\\ \end{matrix} \right] \]
正交投影中的旋转
正交投影过程不涉及object的旋转,因此旋转矩阵\(M_{rotation}\)是单位阵。
此处变换顺序为:先平移再缩放无旋转,因此
$$ M = M_{scale} \dot M_{trans} $$
本文出自CaterpillarStudyGroup,转载请注明出处。
https://caterpillarstudygroup.github.io/GAMES101_mdbook/