滤波 VS 卷积 VS 平均

卷积 VS 平均

结论1： 卷积可以看作是个局部区域的加权平均， 卷积kernel即局部加权

卷积 VS 滤波

🔎 卷积定理：
时域卷积 = 频域乘积
时域乘积 = 频域卷积

图像的卷积操作是从信号的卷积运算中借鉴过来的概念。虽然不完全相同，其本质是一样的。
图像的卷积操作可以看作中对图像的时域信息做卷积运算，时域信息的卷积运算又可以转化为频域上的乘积运算。前面所讲的滤波操作实际上就是用频域上的乘积运算来实现的。因此图像的时域卷积操作与频域滤波操作本质上是一致的。

例子一：以低通滤波为例

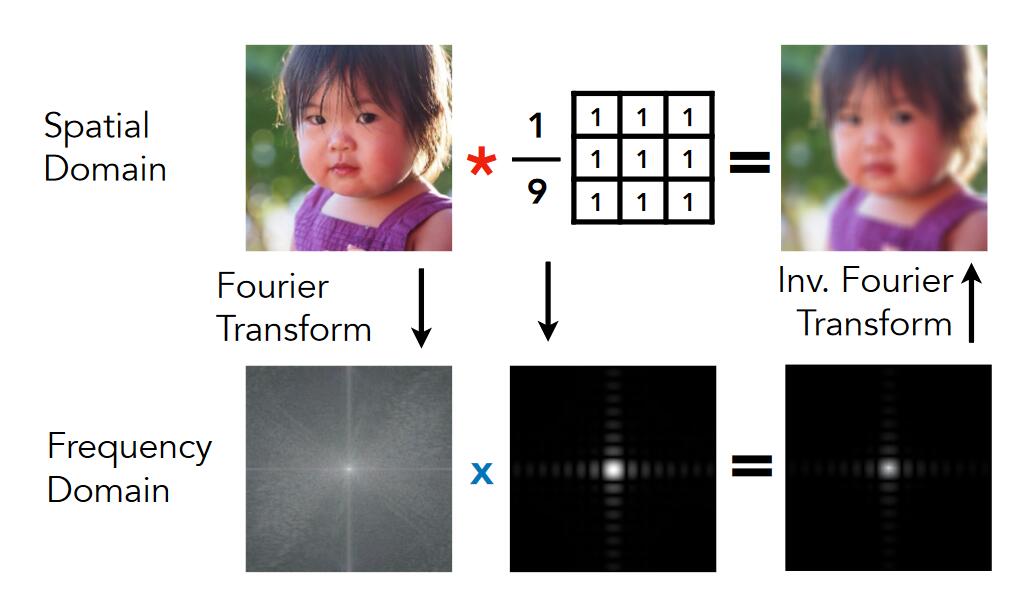
例子二：

❓ 这个例子想说明什么？

结论2：时域卷积 = 频域滤波， 卷积kernel = 频域filter

结论

时域卷积 = 频域滤波 = 局部加权平均

卷积kernel = 频域filter = 局部加权

采样 VS 频域卷积

例子

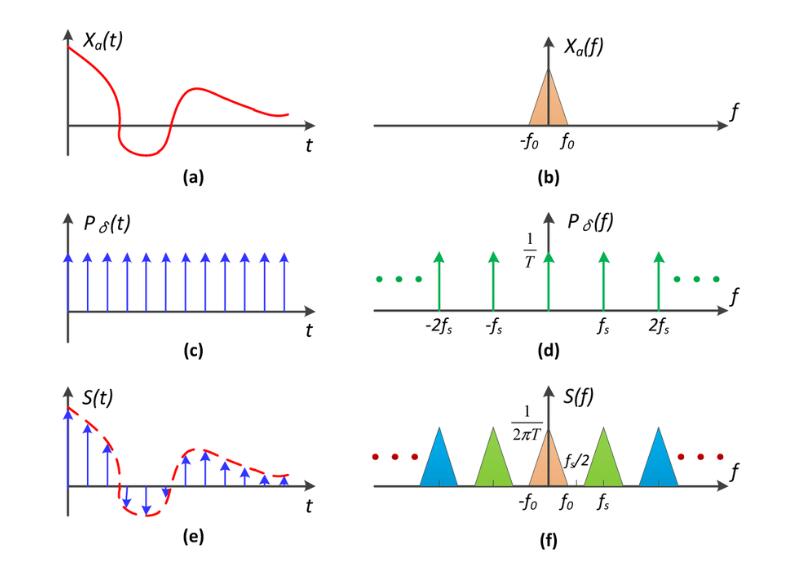
解释：

a：时域信号

b：a对应的频域信号

c：对a进行采样的周期采样函数

d：采样函数的频域表示

e：对a进行采样的结果，即a与c乘积的结果

f：采样结果的频域表示。由于时域乘积=频域卷积，这也是b与d卷积的结果

分析

采样是通过时域上的乘积操作实现的。

时域乘积 = 频域卷积

\[ f_1\left( x \right) \times f_2\left( x \right) \Longleftrightarrow F_1\left( \omega \right) \otimes F_2\left( \omega \right) \]

💡 \(f_1\left( x \right)\) 是信号（a）， \(f_2\left( x \right)\)是采样信号（c）， \(F_1\left( \omega \right)\) 是a的频谱（b） \(F_2\left( \omega \right)\) 是采样信号的频谱

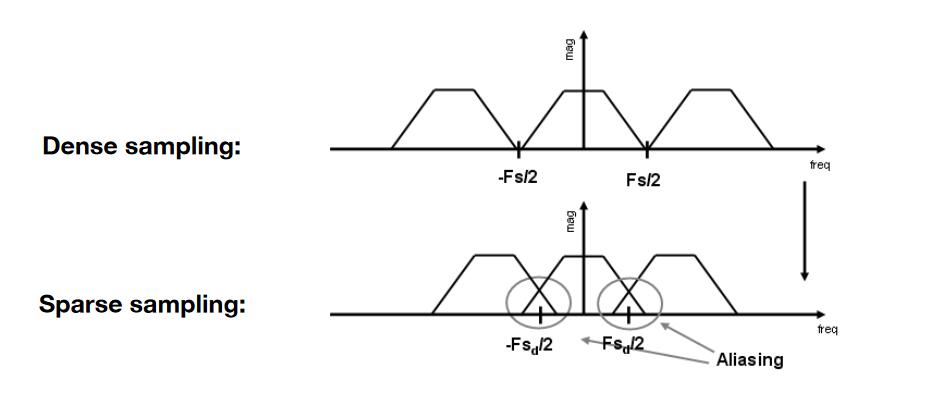
结论：采样就是把原信号的频谱以特定周期呈现。

采样周期长 \(\Longrightarrow \)

\(\Longrightarrow \) \(F_2\left( \omega \right)\) 的频谱间隔小

\(\Longrightarrow \) (b)以更密的形式重复

\(\Longrightarrow \) (f)的频谱出现混叠[55:59]

\(\Longrightarrow \) 时域上表现为走样

本文出自CaterpillarStudyGroup，转载请注明出处。
https://caterpillarstudygroup.github.io/GAMES101_mdbook/