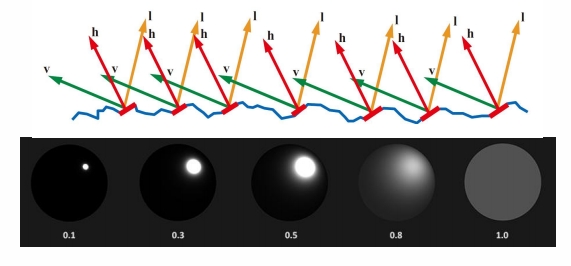
微表面模型 Micro facet Material
当物体很远很小时,从远处看, 是平面且粗糙的。从近处看,是几何且镜面反射。
从微观上看,每个几何表面都有各自的法线方向。但拉远后,这些法线方向就抽象成了法线方向的分布。
💡 本身是随机的,适用统计分布。本身是规律的,可以用公式计算规律。也有可能同一件事,从不同角度去看,会得到随机和有规律两种不同的结论。分析出的规律,也有可能最终还是以统计的方式体现。
微表面的粗糙成度可以用法线分布来表示:
- 当微表面的法线方向比较集中,材质就类似于glossy
- 当微表面的法线方向比较分散,材质就类似于diffuse
BRDF Model Based on Microfacet

$$
L_o(x,\omega _o)=\int _{H^2}\begin{pmatrix}
k_d\frac{c}{\pi } +\frac{DFG}{4(\omega _o\cdot n)(\omega _i\cdot n)}
\end{pmatrix} L_i(x,\omega _i)(\omega _i\cdot n)dw_i
$$
diffuse:漫反射与 Bling Phong 类似,简化成常数。specular:高光,比 Bling Phong 要复杂,其中 D 项与之类似。
DFG 中每个字母代表一种光学现象。
💡 用物理方法模拟的难点在于如何基于物理去建模。用简体近似的方法模拟,难点在于应对简化不合理地方出现的失真。用数据模拟,难点在于大量高质量的数据。
光追属于第一种,这里的方法属于第二种,机器学习属于第三种。
Normal Distribution Function 法向分布方程
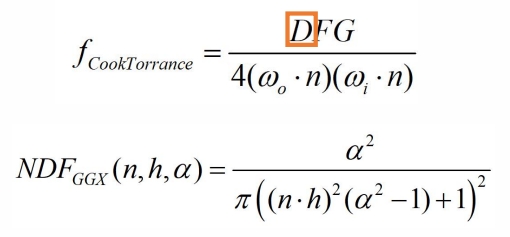
\(\alpha \) 代表 roughness,范围取 [0,1]
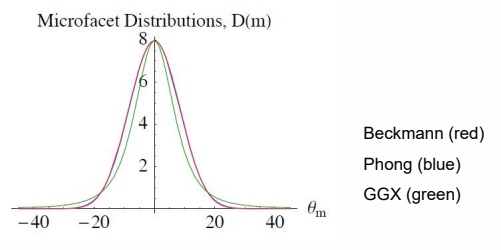
GGX 曲线的特点:高频更具表现力,低频不会那么快消失。
Geometric Attenuation Term (self-shadowing)由于表面不平导致的自遮挡

遮挡影响的特点:
(1) 遮挡可能发生在入射光射向物体表面,也发生在反射光射向眼睛,因此要算两遍。
(2) 与是入射光还是反射光无关
(3) 与入/反射光与法线的夹角有关
(4) 与 D 方式中的 (\( \alpha \)) 有关

Fresnel Equation
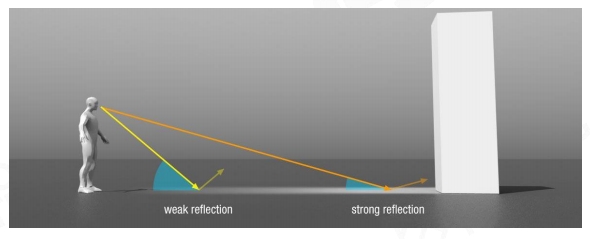
当视线与物体表面的切平面夹角很小时,反射系数会急巨增加,看到倒影效果。
参数:\(\alpha \),fresnel 系数
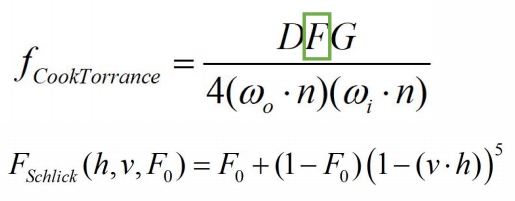
Physical Measured Material


一个关于真实材质的各项系数的数据集。
本文出自CaterpillarStudyGroup,转载请注明出处。
https://caterpillarstudygroup.github.io/GAMES101_mdbook/