当观测结束后，所有物体到了[-1, 1]的三次方这个立方体中，那么，下一步是什么？将其放在屏幕上。

[14:40] 什么是光栅化

🔎
pixel：像素，picture element，一个小方块，且方块内颜色不变
Raster:屏幕，由像素组成二维数组
Rasterize: 光栅化
Triangle Mesh: 三角形面片

光栅化，即把对象（object）画在屏幕（raster）上。对象是指cubic中的内容，常用三角形面片表示对象的表面。屏幕，由像素（pixel）组成的2D数组。数组的大小代码的屏幕的分辨率。
具体过程可以描述为：找到对象表面在cubic中的位置，根据cubic与raster的关系，确定它在raster上应出现的位置。在raster的正确的位置上渲染对象。

将观测的物体在屏幕上显示，就是光栅化。

定义屏幕空间

在屏幕上的坐标系

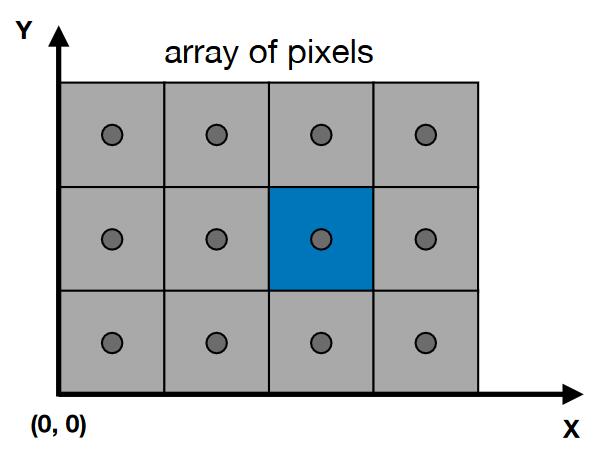
原点在左下角，向右为x正方向，向上为y正方向
每个像素的坐标是整数，范围为[0, width) [0, height)
像素(x， y)的中心位置：(x+0.5, y+0.5)

❗注意区分坐标与位置的不同含义

📌课程中关于显示器的部分被我跳过了，因为我认为与算法相关度不大。

光栅化的最基本的流程

Step 1: 选取cubic中物体的表面三角形

3D空间中的物体，通常使用三角形面片来描述物体的表面。所谓把物体画到屏幕上，实际上就是把这些三角形面片画到屏幕上。

为什么用三角形描述物体表面？

三角形是最基本的多边形（其他多边形可以由三角形拼成）
一个三角形一定在一个平面上
三角形关于“内”、“外”的定义是明确的
给定三角形三个顶点的属性，其内部任意点的属性可以通过插值得出

Step 2: 根据三角形在cubic内的坐标计算出它在屏幕上的位置（浮点数）

坐标系的变换，只需要计算出正确的变换矩阵就可以实现。

\[ \begin{bmatrix} x' \\ y' \\ 1 \\ 1 \\ \end{bmatrix} = \begin{bmatrix} S & T \\ 0 & 1 \\ \end{bmatrix}\begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} \]

其中S是指缩放，T是指平移，这里面不涉及到旋转。

对变换做以下假设：

忽略Z轴
将xy平面：[-1,1]^2 转换到 [0, width] X [0, height]
不涉及旋转

选取部分特殊点，代入计算，即可得出变换矩阵为：

\[ M_{viewport}=\left( \begin{matrix} \frac{width}{2}& 0& 0& \frac{width}{2}\\ 0& \frac{height}{2}& 0& \frac{height}{2}\\ 0& 0& 1& 0\\ 0& 0& 0& 1\\ \end{matrix} \right) \]

Step 3: 把三角形画在屏幕上

根据上面的转换公式，可以得出三角形上每个点对应在屏幕上的位置（浮点数）。但屏幕上像素的下标是整数。如下图：

怎么确定每个像素格子是否需要被渲染成三角形的颜色？
最简单的方法是：判断屏幕空间中每个像素的中心是否在三角形的内部。

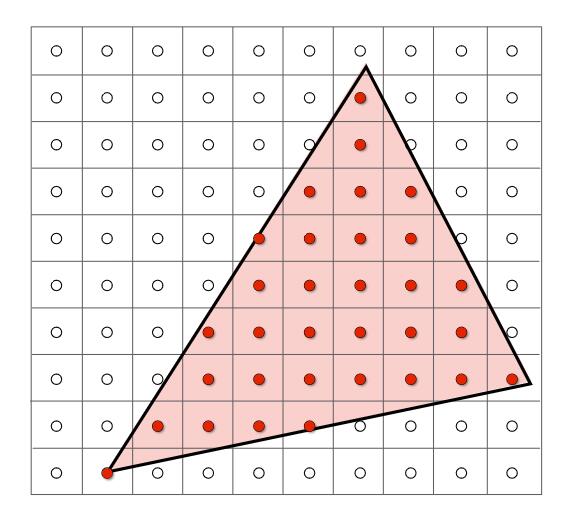
方法一：采样方法

依次遍历每个像素(x, y)：
    取像素中心的位置(x+0.5, y+0.5)
    判断像素中心是否在三角形内部（叉乘）
    如果在内：
        渲染
    如果在外：
        渲染
    如果在三角形边上：
        自己决定是否渲染

🔎判断三角形的内和外：
https://caterpillarstudygroup.github.io/GAMES101_mdbook/Dependency/Vector.html#%E5%9C%A8%E5%9B%BE%E5%BD%A2%E5%AD%A6%E4%B8%AD%E7%9A%84%E4%BD%9C%E7%94%

缺点：必须要依次check每个pixel