问题描述

现象

纹理像素分辨率过大，比被贴图的表面更精细，也会出现问题。例如：

👆 左：期待效果右：实际效果

原因

由于透视的原因，不同距离的屏幕像素对应的纹理像素区域不同

👆 有的像素对应一小部分纹理像素，有的像素对应较大区域的纹理像素

在近处，物体表面比纹理图更精细，即Texture Magnification问题，见上一页，表现为锯齿。

🔎Texture Magnification

在远处，纹理图比物体表面精细，一个屏幕像素对应一片纹理像素，但只取一个纹理像素来代表这一片点，也会出现问题，表现为摩尔纹

进一步解释，从纹理图中取一个texel的过程可以看作是对纹理图的采样。alias的本质是信号变化过快而采样跟不上信号变化的速度。纹理的变化快而采样点稀疏就导致了这种现象。

💡 两个空间的映射，任何一方的不匹配都会现alias，那就对变化快的一块做平均，或对变化慢的一方做细分。

解决方法一：超采样 MSAA

🔎MSAA

原理

对于远处的一个点，取512个texel的value的平均值。

效果

局限性

可解决，但costly。

解决方法二： Mip map[44:20]

原理

点查询（采样）-->范围查询（取一个范围的平均）。

📌
范围查询的应用场景非常广泛，除了CG，还有其它很多领域会用到。
范围查询的目标也有多种，例如取范围内的最大值、最小值、平均值。在这里要查的是平均值。
范围查询的算法也有很多种，在当前场景下使用同MIP Map算法来做范围平均值的查询。

Mip Map算法

作用：用于范围内平均值的查询
特点：快，不精确（近似），只能查询正方形区域

原始纹理称为第0层纹理，根据第0层纹理预先生成出第1-7层纹理。每一层都是上一层缩小一倍。1-7层低分辨率纹理总共仅消耗额外1/3存储。

[47:17]
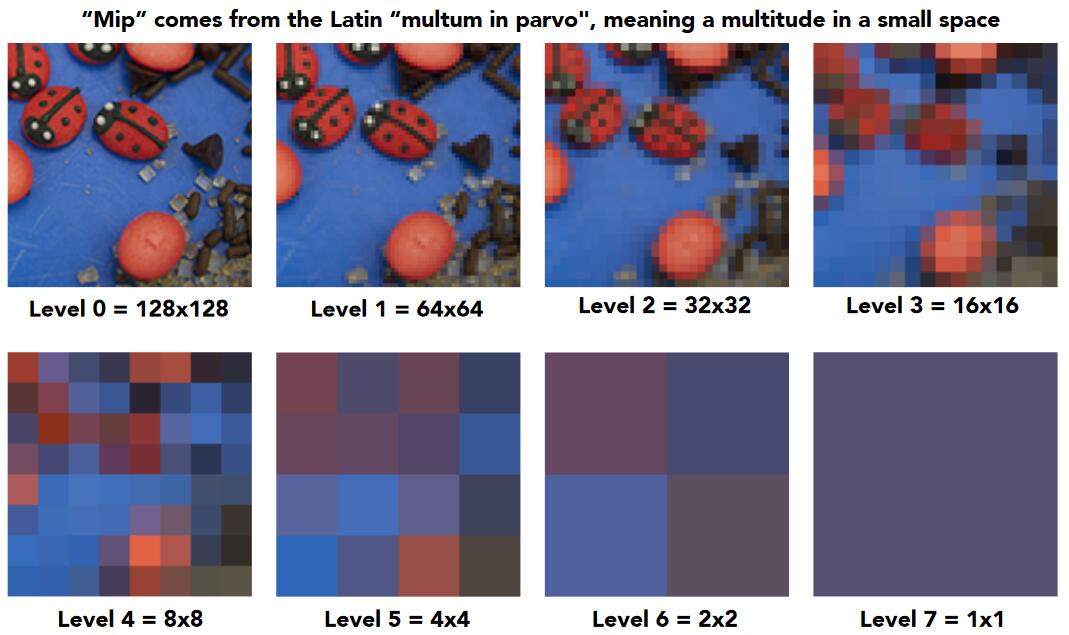
找出屏幕上的一个像素对应的纹理上的近似方形区域。

[52:30]

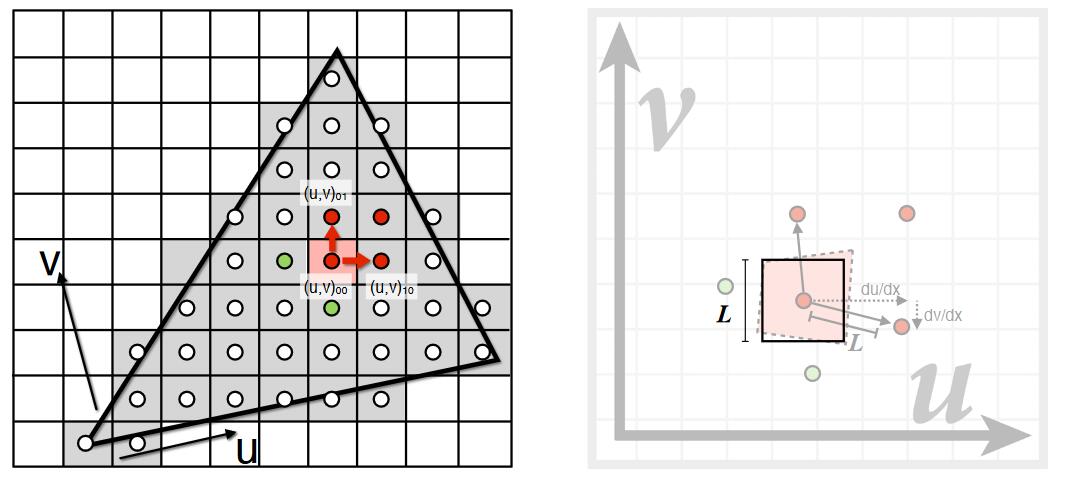
第一步：画出像素对应的四边形区域

已知某像素及其邻居像素对应的texel的位置。像素与上面邻居像素对应的texel位置的中线，认为是像素对应的texel的上边界。
以这种方法，可以在纹理上画出一个不规则四边形区域。

第二步：用一个正方形来近似这个不规则四边形区域。

边长L为：

$$ L = \max(\sqrt{(\frac{du}{dx})^2+(\frac{dv}{dx})^2}, \sqrt{(\frac{du}{dy})^2+(\frac{dv}{dy})^2}) $$

❓ 问：这个公式没有看懂。x和y分别是指什么呢？公式里的变化量是什么呢？是什么和什么之间取最大值？
✅ 答：x和y分别是两个邻居。L是当前texel与两个邻居之间的距离的最大值。（为什么是两个？为什么是这两个邻居？）公式中的两项，分别代表当前texel和x、y的距离。距离是用勾股定理算出来的。里面的微分量是当前texel到邻居的位置变化，分别对应横轴的变化和纵轴的变化。
这只是一种近似方法。可以用其它达到近似目的的方法。