LASSO的原理与Ridge相同，只是在怎么表达theta方面选择了一个不同的指标。

LASSO: Least Absolute Shrinkage and Selection Operator Regression

LASSO的效果

使用与8-8相同的测试数据

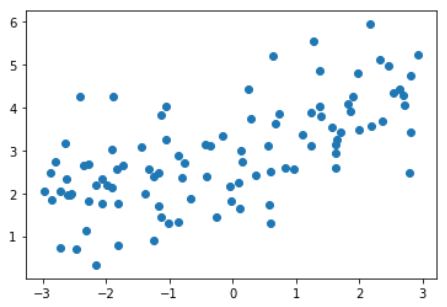
LASSO回归，degree = 20

训练模型

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Lasso

def LassoRegression(degree, alpha):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lasso_reg", Lasso(alpha=alpha))
    ])

from sklearn.model_selection import train_test_split
np.random.seed(666)
X_train, X_test, y_train, y_test = train_test_split(X, y)

from sklearn.metrics import mean_squared_error

lasso1_reg = LassoRegression(degree=20, alpha=0.01)
lasso1_reg.fit(X_train, y_train)

y1_predict = lasso1_reg.predict(X_test)
mean_squared_error(y_test, y1_predict)

MSE = 1.149608084325997

绘制模型

def plot_model(model):
    X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
    y_plot = model.predict(X_plot)

    plt.scatter(x, y)
    plt.plot(X_plot[:,0], y_plot, color='r')
    plt.axis([-3, 3, 0, 6])
    plt.show()

plot_model(lasso1_reg)

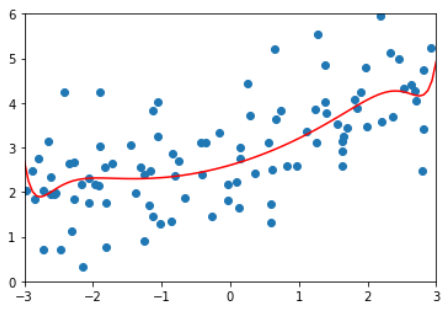
degree=20, 多项式回归、LASSO回归alpha取不同参数的结果对比

| MSE | 拟合曲线 --|---|-- 多项式回归，degree = 20 | 167.94010867772357 | 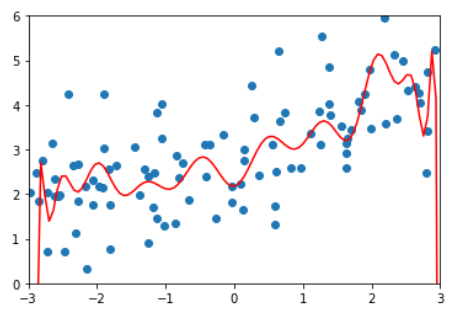LASSO，degree=20，alpha=0.01 | 1.149608084325997 |
LASSO，degree=20，alpha=0.1 | 1.1213911351818648 |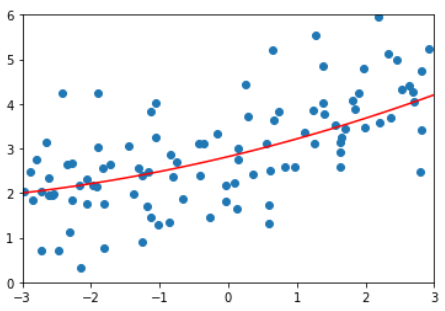
LASSO，degree=20，alpha=1 | 1.8408939659515595 |

Ridge VS. LASSO

在ridge算法中，随着a的增大，曲线越来越平缓，但它始终是一条曲线。
但在lasso算法中，a取0.1时模型已经接近是直线了。
使用lasso模型得到的更倾向于是一根直线。

直线与曲线的区别在于x的系数theta是否为0。使用lasso中会导致很多特征的系数为0。

lasso趋向于使得一部分theta值变为0，所以可作为特征选择用。
因为如果使用lasso后一部分特征的theta变为0，就代表lasso认为这部分特征是没有用的。

造成ridge和lasso这种区别的原因与它们的导数形式有关。

lasso算法可能会错误地将有用的特征也变为0，从计算准确度角度讲，ridge更准确。
但如果特征数量特别大，使用lasso可以让特征变少。