超参数和模型参数

超参数是指运行机器学习算法之前要指定的参数
KNN算法中的K就是一个超参数

模型参数：算法过程中学习的参数
KNN算法没有模型参数

调参是指调超参数

如何寻找好的超参数

领域知识
经验数值
实验搜索

寻找最好的K

best_score = 0.0
best_k = -1
for k in range(1, 11):
    knn_clf = KNeighborsClassifier(n_neighbors=k)
    knn_clf.fit(X_train, y_train)
    score = knn_clf.score(X_test, y_test)
    if score > best_score:
        best_k = k
        best_score = score

print("best_k = ", best_k)
print("best_score = ", best_score)

输出：
best_k = 4
best_score = 0.9916666666666667

KNN的超参数weights

普通的KNN算法：蓝色获胜
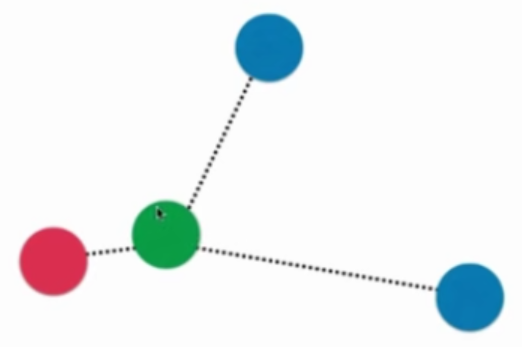
考虑距离的KNN算法：红色：1，蓝色：1/3 + 1/4 = 7/12，蓝色获胜

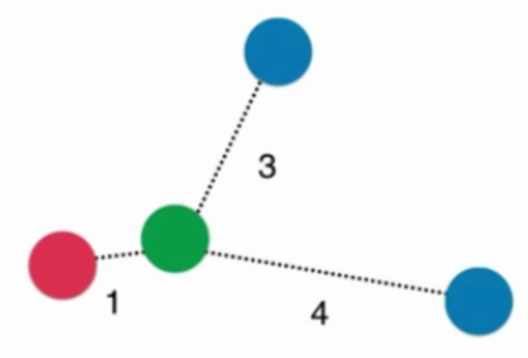
考虑距离的另一个优点：解决平票的情况

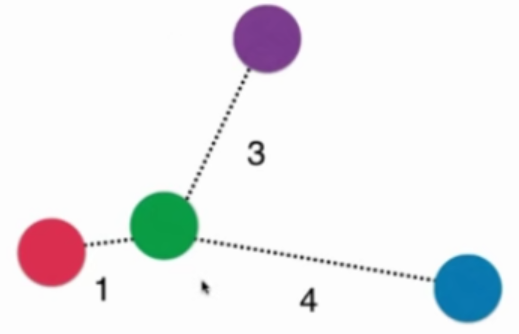
best_method = ""
best_score = 0.0
best_k = -1
for method in ["uniform", "distance"]:
    for k in range(1, 11):
        knn_clf = KNeighborsClassifier(n_neighbors=k, weights=method)
        knn_clf.fit(X_train, y_train)
        score = knn_clf.score(X_test, y_test)
        if score > best_score:
            best_k = k
            best_score = score
            best_method = method

print("best_k = ", best_k)
print("best_score = ", best_score)
print("best_method = ", best_method)

输出结果：
best_k = 4
best_score = 0.9916666666666667
best_method = uniform

KNN的超参数p

关于距离的更多定义

欧拉距离

$$ \sqrt {\sum^n_{i=1} (X^{(a)}_i-X^{(b)}_i)^2} $$

曼哈顿距离

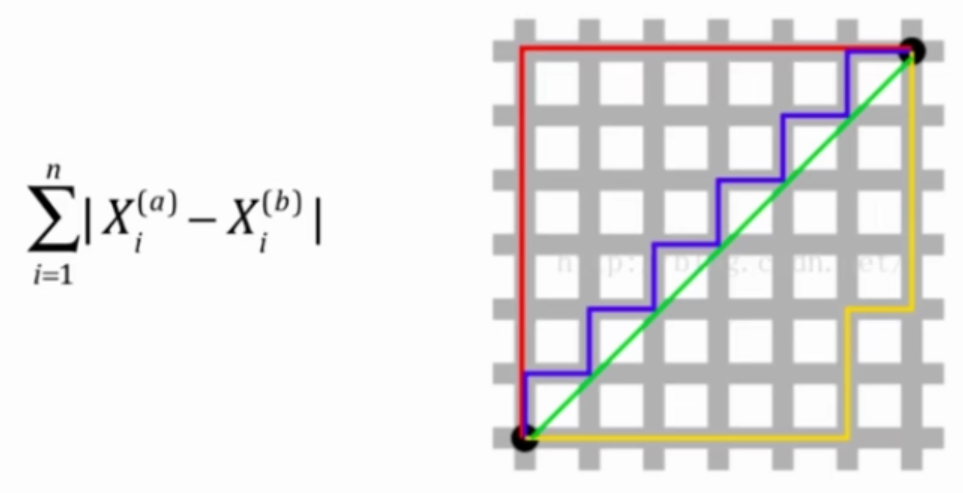
欧拉距离与曼哈顿距离的数学形式一致性

$$ (\sum^n_{i=1} |X^{(a)}_i-X^{(b)}_i|^2)^\frac{1}{2} $$

$$ (\sum^n_{i=1} |X^{(a)}_i-X^{(b)}_i|)^\frac{1}{1} $$

明可夫斯基距离 Minkowski distance

$$ (\sum^n_{i=1} |X^{(a)}_i-X^{(b)}_i|^p)^\frac{1}{p} $$

把欧拉距离和曼哈顿距离进一步抽象，得到以下公式

p = 1: 曼哈顿距离
p = 2: 欧拉距离
p > 2: 其他数学意义

%%time

best_p = -1
best_score = 0.0
best_k = -1

for k in range(1, 11):
    for p in range(1, 6):
        knn_clf = KNeighborsClassifier(n_neighbors=k, weights="distance", p = p)
        knn_clf.fit(X_train, y_train)
        score = knn_clf.score(X_test, y_test)
        if score > best_score:
            best_k = k
            best_score = score
            best_p = p

print("best_k = ", best_k)
print("best_score = ", best_score)
print("best_p = ", best_p)

输出结果：
best_k = 3
best_score = 0.9888888888888889
best_p = 2
Wall time: 37 s

LYBStudy