线性回归要求数据存在线性关系。
但实际场景中，存在强线性关系的数据是比较少的，大部分情况下数据之间是非线性关系。
用一种简单的手段改进线性回归法，使得它可以处理和预测非线性数据。
即多项式回归。

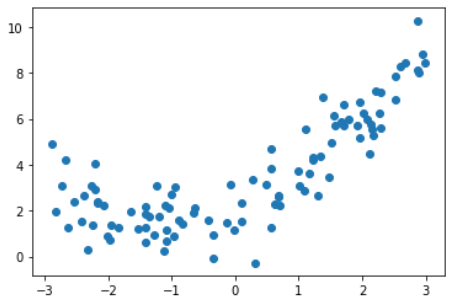
准备数据

import numpy as np
import matplotlib.pyplot as plt

x = np.random.uniform(-3, 3, size=100)
X = x. reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)

plt.scatter(X, y)
plt.show()

使用线性回归

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X, y)
y_predict = lin_reg.predict(X)

plt.scatter(x, y)
plt.plot(x, y_predict, color='r')
plt.show()

解决方案， 添加一个特征

X2 = np.hstack([X, X**2])

lin_reg2 = LinearRegression()
lin_reg2.fit(X2, y)
y_predict2 = lin_reg2.predict(X2)

plt.scatter(x, y)
plt.plot(np.sort(x), y_predict2[np.argsort(x)], color='r')
plt.show()

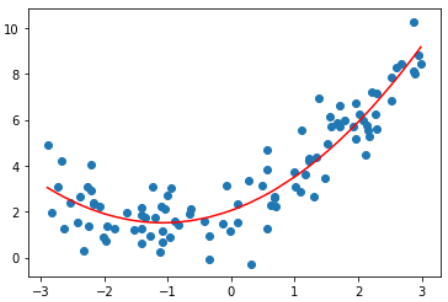
看上去这根曲线拟合得更好。

输入：lin_reg2.coef_
输出：array([0.99902653, 0.46334749])
0.999是x的系数，0.46是x^2的系数

输入：lin_reg2.intercept_
输出：2.0518267069340164

结论

使用线性回归的思路，为原来的样本添加新的特征，新的特征是原有特征的多项式的组合。以此来解决非线性问题。

PCA是对数据做降维处理，这里则是对数据集升维。通过升维和添加特征，使算法拟合高维度的数据。