2019-10-19

KNN - K近邻算法 - K-Nearest Neighbors

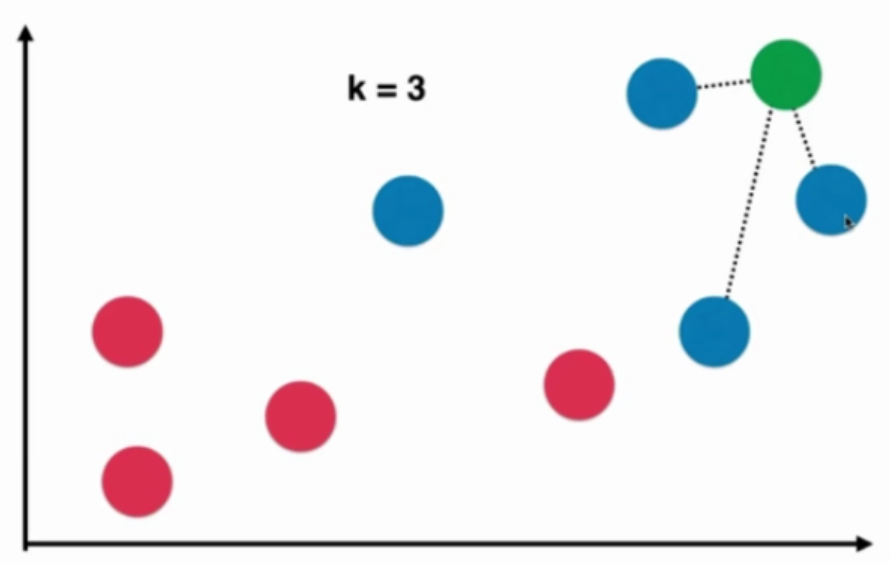
本质：如果两个样本足够相似，它们有更高的概率属于同一个类别

代码实现KNN算法

假设原始训练数据如下：

raw_data_X = [[3.39, 2.33],
              [3.11, 1.78],
              [1.34, 3.36],
              [3.58, 4.67],
              [2.28, 2.86],
              [7.42, 4.69],
              [5.74, 3.53],
              [9.17, 2.51],
              [7.79, 3.42],
              [7.93, 0.79]
             ]
raw_data_y = [0, 0, 0, 0, 0, 1, 1, 1, 1, 1]

待求数据如下：

x = np.array([8.09, 3.36])

数据准备

import numpy as np
import matplotlib.pyplot as plt

X_train = np.array(raw_data_X)
y_train = np.array(raw_data_y)

plt.scatter(X_train[y_train==0, 0], X_train[y_train==0, 1], color = 'g')
plt.scatter(X_train[y_train==1, 0], X_train[y_train==1, 1], color = 'r')
plt.scatter(x[0], x[1], color = 'b')
plt.show()

效果：

KNN过程

欧拉距离

假设有a, b两个点，平面中两个点之间的欧拉距离为:

$$\sqrt {(x^{(a)}-x^{(b)})^2+(y^{(a)}-y^{(b)})^2}$$

立体中两个点的欧拉距离为:

$$\sqrt {(x^{(a)}-x^{(b)})^2+(y^{(a)}-y^{(b)})^2+(z^{(a)}-z^{(b)})^2}$$

任意维度中两个点的欧拉距离为:

$$\sqrt {(X^{(a)}_1-X^{(b)}_1)^2+ (X^{(a)}_2-X^{(b)}_2)^2+...+(X^{(a)}_n-X^{(b)}_n)^2}$$

或

$$\sqrt {\sum^n_{i=1} (X^{(a)}_i-X^{(b)}_i)^2}$$

其中上标a, b代码第a, b个数据。下标1, 2代码数据的第1, 2个特征

代码如下：

distances = [np.sum((x_train - x) ** 2) for x_train in X_train]
nearest = np.argsort(distances)
topK_y = [y_train[i] for i in nearest[:k]]
from collections import Counter
votes = Counter(topK_y)
predict_y = votes.most_common(1)[0][0]

运行结果：predict_y = 1