简单线性回归

找一条直线，这条直线最大程度地拟合所有的样本特征点

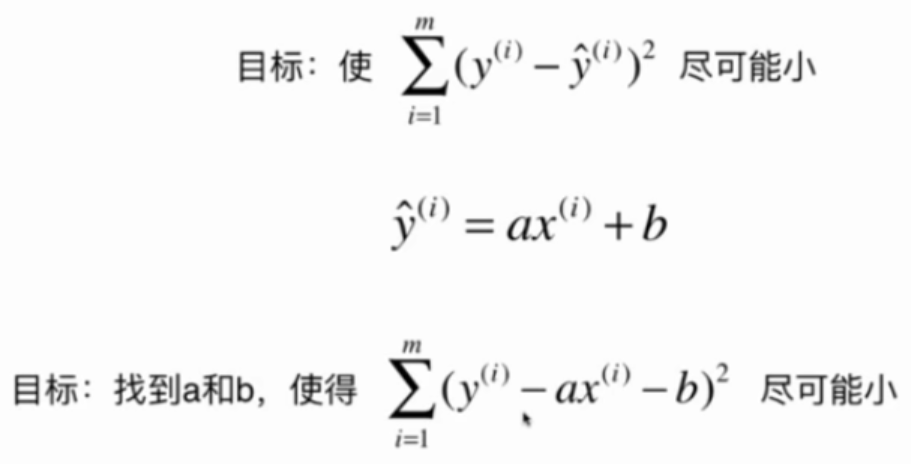
一类机器学习算法的基本思路

通过分析问题，确定问题的损失函数(loss function)或效用函数(utility function), 有时也称为目标函数
通过最优化损失函数或效用函数，获得机器学习的模型

近乎所有的参数学习算法都是这样的套路, e.g. 线性回归, 多项式回归, 逻辑回归, SVM, 神经网络, etc...本质都是在学习相应的参数来最优化目标函数, 区别在于模型不同从而建立的目标函数不同, 优化的方式也不尽相同.

最优化原理
凸优化

目标：找到$${a}$$和$${b}$$，使用$$\sum^m_{i=1}(y^{(i)}-ax^{(i)}-b)^2$$尽可能小。
这是典型的最小二乘法问题：最小化误差的平方
解得：

$$ a = \frac{\sum_{i=1}^m(x^{(i)}-\bar x)(y^{(i)}-\bar y)}{\sum_{i=1}^m(x^{(i)}-\bar x)^2}\quad \quad \quad \quad \quad b = \bar y - a\bar x $$