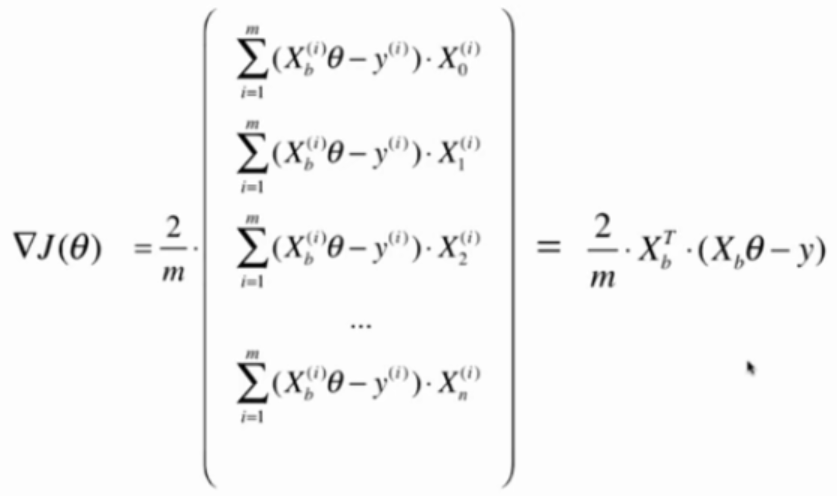
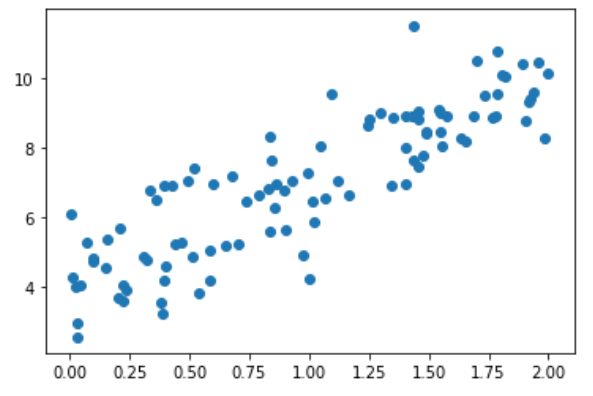
测试数据

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(666)
x = 2 * np.random.random(size=100)
y = x * 3. + 4. + np.random.normal(size=100)

X = x.reshape(-1, 1)

plt.scatter(x, y)
plt.show()

向量化计算dJ

        def dJ(theta, X_b, y):
            return X_b.T.dot(X_b.dot(theta)-y) * 2. / len(X_b)

使用真实数据测试模型

真实数据 + 正规化方程解

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=666)

lin_reg1 = LinearRegression()
lin_reg1.fit_normal(X_train, y_train)  # 见5-4
lin_reg1.score(X_test, y_test)

输出结果：
0.8129794056212832

真实数据 + 梯度下降法

lin_reg2 = LinearRegression()
lin_reg2.fit_gd(X_train, y_train)
lin_reg2.score(X_test, y_test)

输出结果：
eta太大导致搜索过程不收敛

真实数据 + 梯度下降法 + eta=0.000001

lin_reg2 = LinearRegression()
lin_reg2.fit_gd(X_train, y_train, eta = 0.000001)
lin_reg2.score(X_test, y_test)

输出结果：
0.27586818724477247

训练次数不够，没有达到最优值

真实数据 + 梯度下降法 + eta=0.000001 + n_iters=1e6

lin_reg2 = LinearRegression()
lin_reg2.fit_gd(X_train, y_train, eta = 0.000001, n_iters=1e6)
lin_reg2.score(X_test, y_test)

输出结果：
0.7542932581943915

训练次数太多，导致训练时间太长，但次数又不足以找到最优解
解决方法：数据归一化

梯度下降法与数据归一化

多元线性回归问题中，不同特征的规格一样，导致eta很难选。同一个eta可能会导致某些无法收敛而另一特征又收敛太慢。
因此使用梯度下降法之前，最好对数据进行归一化

from sklearn.preprocessing import StandardScaler

standardScaler = StandardScaler()
standardScaler.fit(X_train)

X_train_standard = standardScaler.transform(X_train)
X_test_standard = standardScaler.transform(X_test)

lin_reg3 = LinearRegression()
lin_reg3.fit_gd(X_train_standard, y_train)
lin_reg3.score(X_test_standard, y_test)

输出结果：
0.8129873310487505

LYBStudy