主成分分析法 PCA Principal Component Analysis

一个非监督的机器学习算法
主要用于数据的降维
通过降维，可以发现更便于人类理解的特征
其他应用：可视化，去噪

二维降至一维

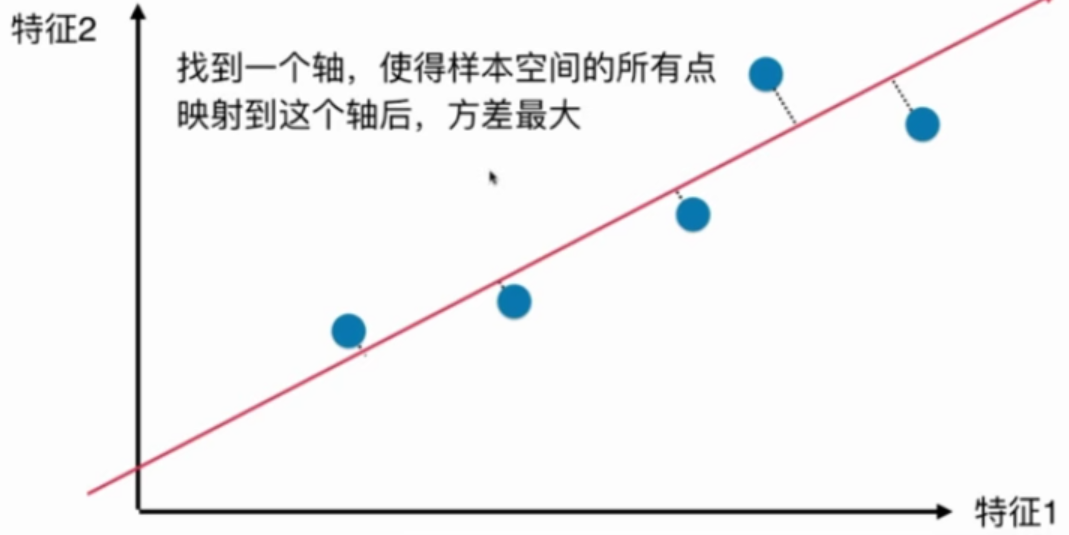
如何把图中的二维空间中的点降至一维？

以上三种方法哪种更好？
第三种，因为第三种最大程度地保留了原数据之间的关系. 概率论与数理统计中, 方差(Variance)描述了样本整体疏密的一个指标.

如何找到这个样本间间距(方差)最大的轴？

$$\begin{aligned} Var(x) = \frac{1}{m}\sum_{i=1}^m(x_i-\bar x)^2 && (1) \end{aligned}$$

其中 $$\bar x$$ 代表x的平均值。

第一步：将所有样本的均值归0 （demean）

由于均值为0，则公式（1）可以化简为:

$$\begin{aligned} Var(x) = \frac{1}{m}\sum_{i=1}^m(x_i-\bar x)^2 = \frac{1}{m}\sum_{i=1}^mx_i^2 && (2) \end{aligned}$$

这里的x是样本映射到坐标轴以后的新的样本的值 $$X_{\text{project}}$$ 。
第二步：求一个轴的方向w = (w1, w2)，使用所有的样本映射到w以后，有 $$Var(X_{\text{project}})$$ 最大:

$$\begin{aligned} Var(X_{\text{project}}) = \frac{1}{m}\sum_{i=1}^m||x^{(i)}_{\text{project}}||^2 && (3) \end{aligned}$$

推导过程：

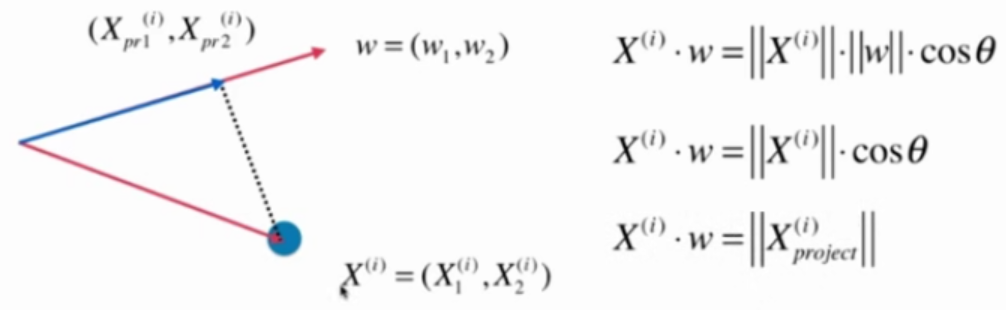
假设均值化之后的x的坐标为

$$X^{(i)}=(X^{(i)}_1, X^{(i)}_2)$$

要映射的坐标轴为 $$w-{w_1, w_2}$$
$$X^{(i)}$$ 映射到 $$w - {w_1, w_2}$$ 之后的新坐标为

$$X_{pr}^{(i)} = (X^{(i)}{pr1}, X^{(i)}{pr2})$$

那么, $$||x^{(i)}_{\text{project}}||$$ 为:

$$||x^{(i)}_{\text{project}}|| = X^{(i)} \cdot w$$

代入公式（3）得:

$$\begin{aligned} Var(X_{\text{project}}) = \frac{1}{m}\sum_{i=1}^m|| X^{(i)} \cdot w||^2 && (4) \end{aligned}$$

目标是最大化公式（4），这是一个求目标函数的最优化问题，使用梯度上升法解决。

主成分分析法和线性回归的区别

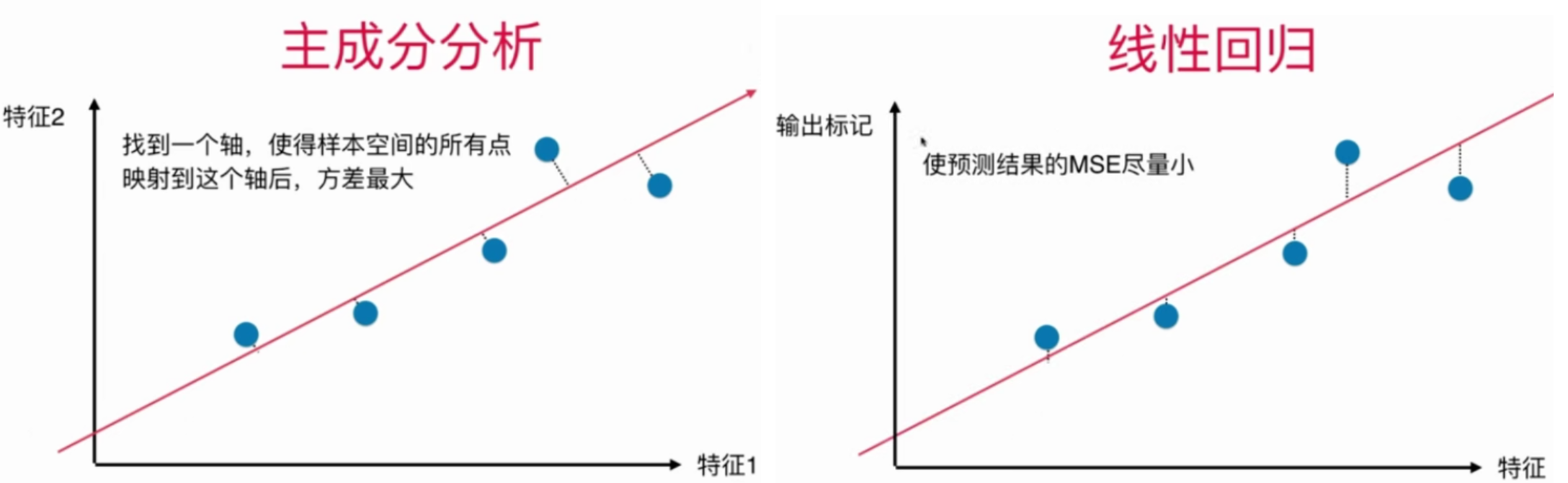
| 主成分分析 | 线性回归 --|---|-- 坐标轴 | 2个特征 | 1个特征和输出标记 要求的是什么 | 一个方向 | 一根直线 经过点的线与什么垂直 | 所求的方向垂直 | x轴 目标 | 方差最大 | MSE最小