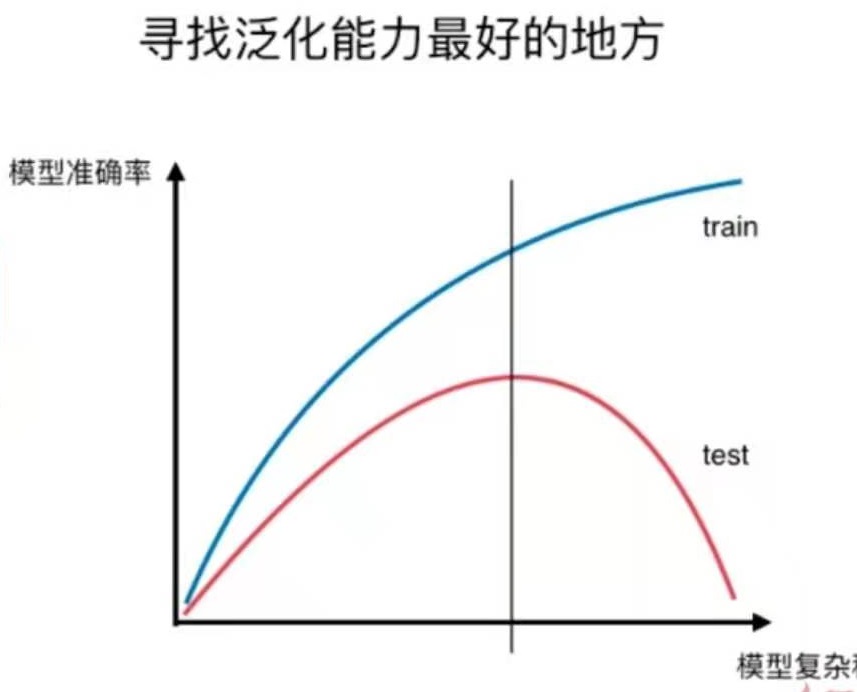
机器学习主要要解决的问题是过拟合问题。
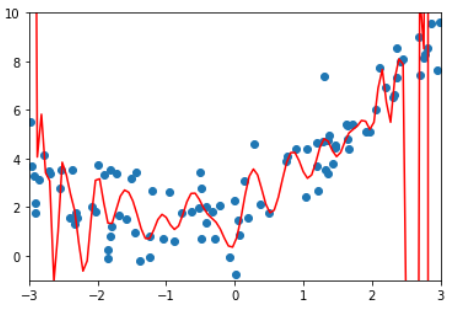
例如这根曲线,虽然这根曲线将样本点拟合得很好,总体误差很低,但如果来了一个新样本,它就不能进行很好的预测了。也就是说,这个模型的泛能力很弱。
泛化能力即由此及彼的能力。
我们训练模型不是为了这些已知的点,而是为也预测。因此模型对训练数据的拟合程度有多好是没有意义的。真正需要的是模型的泛化能力。
解决方法:
训练、测试数据分离。
模型只使用训练数据集获取。测试数据对于模型是全新的数据。
如果模型对于测试数据也有很好的结果,就说模型的泛化能力是很强的。
如果模型对训练数据集的效果好,而对测试数据的效果很差,就说模型的泛化能力很弱,通常是过拟合。
仍使用8-3的数据,degree取不同值时在test数据集上的效果对比
| degree | 在训练数据集上的MSE | 在测试数据集上的MSE | note |
|---|---|---|---|
| 线性 | 3.0750025765636577 | 2.2199965269396573 | |
| 2 | 1.0987392142417856 | 0.80356410562979 | 使用二次模型得到的泛化结果比使用线性模型得到的要好 |
| 10 | 1.050846676376417 | 0.9212930722150768 | 在训练数据集上(8-3)degree取10效果更好,但在测试数据集上degree取10的效果变差了。说明degree取10时它的泛化能力变弱了。 |
| 100 | 0.6880004678712686 | 14075796434.50641 | 在训练数据集上效果最好,在测试数据集上效果极差 |
测试数据集的意义
对于不同的算法,模型复杂度代码不同的意思。
对于多项式回归算法来说,模型复杂度相当于degree,degree越高,模型越复杂。
对于KNN算法来说,K越小,模型越复杂。
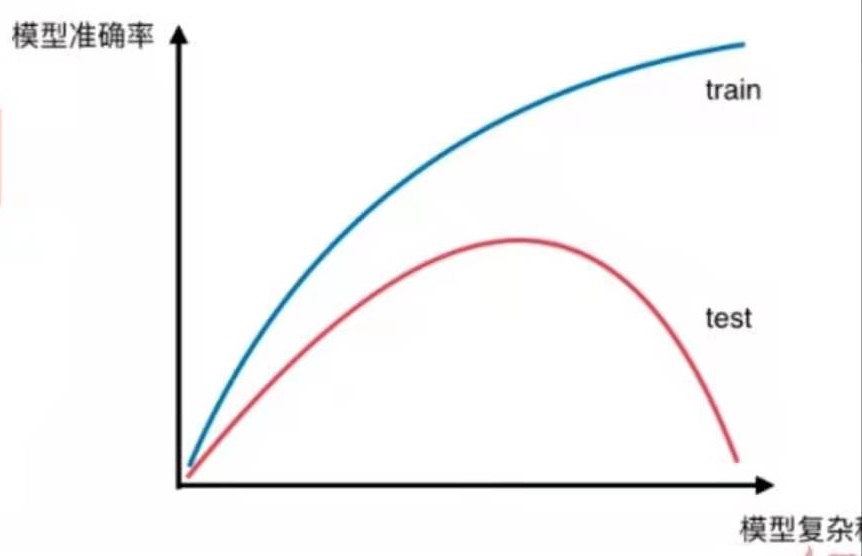
如图所示:
对于训练数据来说,模型越复杂,模型准确率就越高。
对于测试数据来说,模型最简单时,测试数据的准确率会比较低,当模型变复杂时,训练数据的准确率会提升。随着模型越来越复杂,当准确率提升到一定程度时又开始下降。
这就是“欠拟合-合适-过拟合”的过程。
这只是一个示意图,不同模型得到的具体图像不同,但整体上是这样的趋势。
欠拟合 vs 过拟合
欠拟合 underfitting
算法所训练的模型不能完整表述数据关系。
过拟合 overfitting
算法所训练的模型过多地表达了数据间的噪音关系。