SVM要最大化margin,即图中两根直线之间的距离

用数学语言来表达: margin = 2 * d,最大化d就是最大化margin
点x到直线$$w^T * x + b = 0$$的距离为:
$$
distance = \frac{|w^T+b|}{||w||} \
||w|| = \sqrt {w_1^2+w_2^2+\cdots+w_n^2}
$$
所有的样本点到决策边界到距离都应该大于d,用于公式表达:

上面这个公式可写成这样的形式:
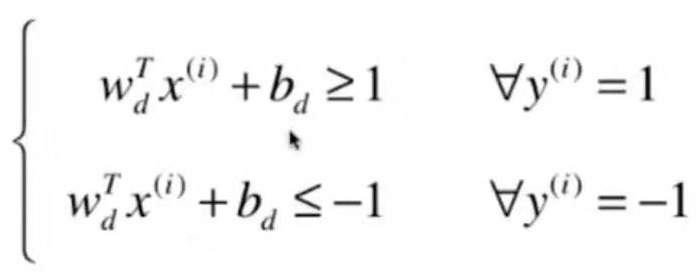
于是可得出margin上下两条直线的方程为:
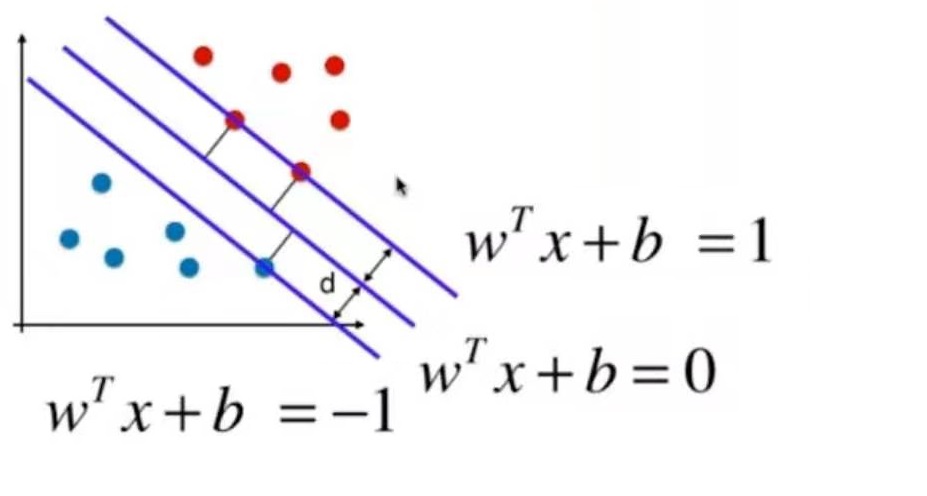
**注意:这里三条直线中的已经不是原来的$$w^T$$和b了,$$w_b^T=w^T/(||w||d), b_d=b/(||w||d)$$
SVM的目标是最大化d,d的公式在上文已经给出。
由于支持向量x一定是在margin的上下边界点上,可以证明对于任意支持向量x,以下四个公式表达的目标的相同的:

结论:
SVM算法演变为有条件的最优化问题,(st:条件)

有条件的最优化问题和没有条件的最优化问题,其求解方法大不相同。