1. 每个结点在哪个维度做划分？
2. 某个维度的哪个值上做划分？
   用信息熵解决以上问题

信息熵

信息熵表示一组变量的不确定度。
熵越大，不确定性越高。
熵越小，不确定性越低。

信息熵的计算公式：

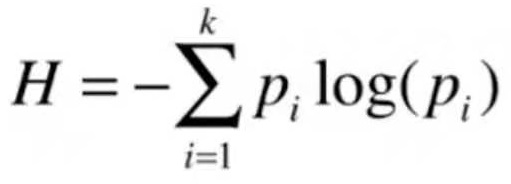
假设数据集中有三个类别，样本属于这三个类别的概率分别是{1/3, 1/3, 1/3}，此时信息熵H为：
H = -1/3log(1/3) -1/3log(1/3) -1/3log(1/3) = 1.0986
如果三个类别的概率分别是{0.1、0.2、0.7}，那么H=0.8018
如果三个类别的概率分别是{1, 0, 0}，那么H=0

以二分类为例，画出信息熵的图像

数据只有两个类型，其中一类的概率为x，信息熵计算公式如下：

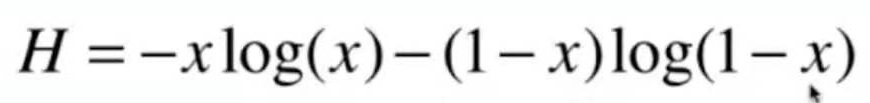
import numpy as np
import matplotlib.pyplot as plt

def entropy(p):
    return -p * np.log(p) - (1-p) * np.log(1-p)

x = np.linspace(0.01, 0.99, 200)

plt.plot(x, entropy(x))
plt.show()

数据是任何一个类别的概率是一样大时，信息熵最大。
系统偏向于某一类，信息熵降低。
当数据100%确定是某一类时，信息熵为0

总结：

每一次划分时，让划分后的信息熵为所有划分结果的最低。