梯度的求解并不容易，如果知道自己求的梯度是否正确？

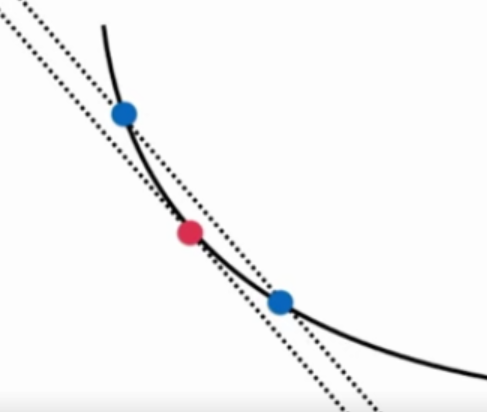
图中两条直线的斜率近乎相等。
两个蓝点越接近，斜率越相近。

推广到高维场景

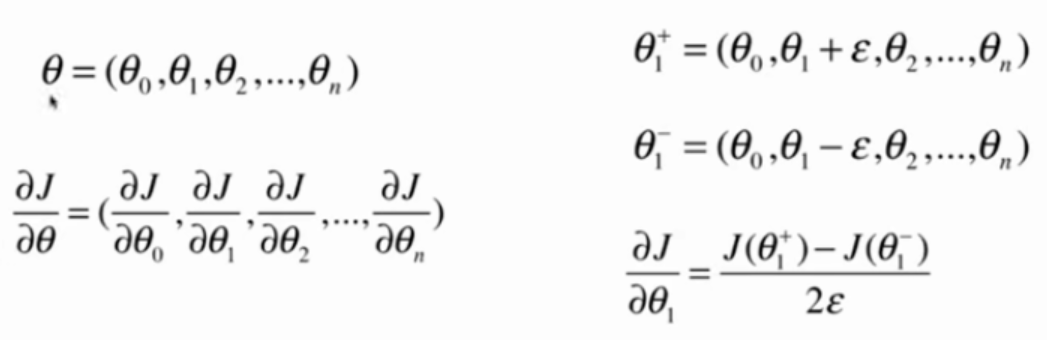
代码实现

准备数据

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(666)
X = np.random.random(size=(1000, 10))
true_theta = np.arange(1, 12, dtype=float)
X_b = np.hstack([np.ones((len(X), 1)), X])
y = X_b.dot(true_theta) + np.random.normal(size=1000)

def J(theta, X_b, y):
    try:
        return np.sum((y - X_b.dot(theta))**2) / len(X_b)
    except:
        return float('inf')

两种方法求导数

def dJ_math(theta, X_b, y):
    return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)

def dJ_debug(theta, X_b, y, epsilon=0.01):
    ret = np.empty(len(theta))
    for i in range(len(theta)):
        theta_1 = theta.copy()
        theta_1[i] +=epsilon
        theta_2 = theta.copy()
        theta_2[i] -=epsilon
        ret[i] = (J(theta_1, X_b, y) - J(theta_2, X_b, y)) / (2*epsilon)
    return ret

两种方法训练模型

def gradient_descent(dJ, X_b, y, initial_theta, eta, n_iters = 1e4, epsilon=1e-8):
    theta = initial_theta
    i_iter = 0
    while i_iter < n_iters:
        gradient = dJ(theta, X_b, y)
        last_theta = theta
        theta = theta - eta * gradient
        if (abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
            break
        i_iter += 1
    return theta

X_b = np.hstack([np.ones((len(X), 1)), X])
initial_theta = np.zeros(X_b.shape[1])
eta = 0.01

%time theta = gradient_descent(dJ_debug, X_b, y, initial_theta, eta)
%time theta = gradient_descent(dJ_math, X_b, y, initial_theta, eta)

实验结果

dJ_math对应的运行时间为：660 ms
dJ_debug对应的运行时间为：4.58s
两种方法求出的theta完全相同

dJ_debug的方法可以用于求梯度，最终能得到正确的结果
dJ_debug速度很慢。
可以先使用dJ_debug得到想要的正确结果。
再用dJ_math将得到的结果与dJ_debug的结果相比较，来验证数学是否正确。
dJ_debug与J无关，可以适用于所有函数。