先回顾一下上一节课的代码

import numpy as np
from sklearn import datasets

digits = datasets.load_digits()
X = digits.data
y = digits.target.copy()

y[digits.target==9] = 1
y[digits.target!=9] = 0

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

from sklearn.linear_model import LogisticRegression

log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
log_reg.score(X_test, y_test)

输出：0.9755555555555555

skleran的Logical Regression中，通过discision score和threshold来判断分类结果。
默认情况下threshold = 0。
调整threshold值，精准率和召回率就会相应的变化。
这一节通过可视化的方式表现threshold和精准率、召回率之间的关系。

精准率和召回率的变化曲线

decision_scores = log_reg.decision_function(X_test)

from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
import matplotlib.pyplot as plt

precision_scores = []
recall_scores = []

thresholds = np.arange(np.min(decision_scores), np.max(decision_scores), step=0.1)
for threshold in thresholds:
    y_predict = np.array(decision_scores >= threshold, dtype='int')
    precision_scores.append(precision_score(y_test, y_predict))
    recall_scores.append(recall_score(y_test, y_predict))

plt.plot(thresholds, precision_scores)
plt.plot(thresholds, recall_scores)
plt.show()

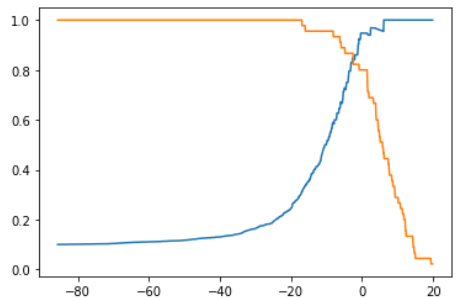
可以根据这张图找到想要的threshold。

绘制precision-recall曲线

plt.plot(precision_scores, recall_scores)
plt.show()

scikit-learn中的precision-recall曲线

from sklearn.metrics import precision_recall_curve

precisions, recalls, thresholds = precision_recall_curve(y_test, decision_scores)
plt.plot(thresholds, precisions[:-1])
plt.plot(thresholds, recalls[:-1])
plt.show()

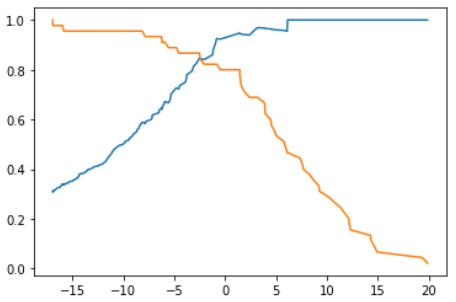
Note 1:precisions.shape = (145,)，recalls.shape = (145,)，thresholds.shape = (145,)，这是因为“the last precision and recall values are 1. and 0. respectively and do not have a corresponding threshold.”

Note 2：sklearn提供的precision-recall曲线自动只寻找了我们最关心的那一部分。

关于precision-recall曲线的理论说明

召回率急剧下降开始的点通常精准率-召回率最好的平衡点。

精准率-召回率曲线整体上是这样的曲线。用不同的算法或相同的算法的不同的超参数都能训练出各自的模型。每种模型都有不同的精准率-召回率曲线。
假如如图是两个模型的精准率-召回率曲线，那么明显可以得出结论外面曲线的模型优于里面曲线的模型。因此PR曲线也可以作为选择模型/超参数的指标。