分类问题使用accuracy来评价分类结果。
回归问题怎样评价预测结果？

MSE RMSE MAE

均方误差 MSE Mean Squared Error

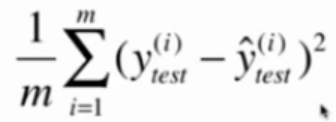
问题：量纲

均方根误差 RMSE Root Mean Squared Error

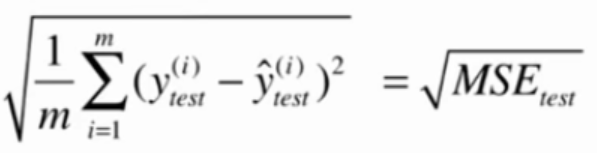与MSE本质上是一样的
放大了最大的错误

平均绝对误差 MAE Mean Absolute Error

训练过程中，没有把这个函数定义成目标函数，是因为它不是处处可导。
但它仍可以用于评价算法
评价一个算法所使用的标准可以和训练时所用的标准不同

编程实现三种

波士顿房产数据

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

boston = datasets.load_boston()
x = boston.data[:, 5] # 5代码房间数，保使用房间数量这个特征
y = boston.target

plt.scatter(x, y)
plt.show()

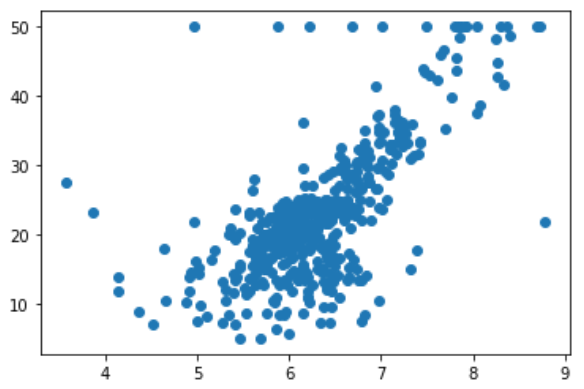
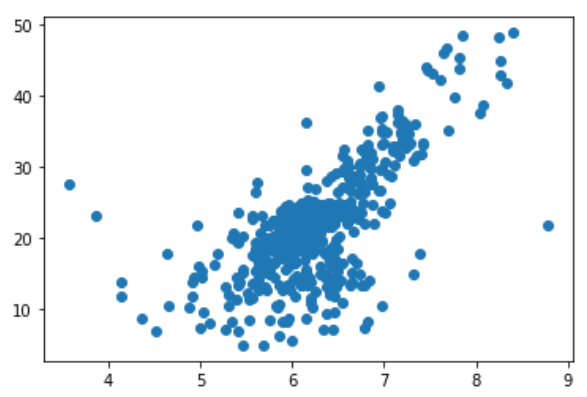
图中最上面有一排点比较奇怪，把它们去掉

x = x[y < 50.0]
y = y[y < 50.0]
plt.scatter(x, y)
plt.show()

训练模型，预测结果

from sklearn.model_selection import train_test_split
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=666)

reg = SimpleLinearRegression()  #见5-4
reg.fit(x_train, y_train)

plt.scatter(x_train, y_train)
plt.plot(x_train, reg.predict(x_train), color='r')
plt.show()

评价预测效果

y_predict = reg.predict(x_test)

mse_test = np.sum((y_predict - y_test) ** 2) / len(y_test)

from math import sqrt
rmse_test = sqrt(mse_test)

mae_test = np.sum(np.absolute(y_predict-y_test)) / len(y_test)

使用scikit-learn中的MSE和MAE

from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error

mean_squared_error(y_test, y_predict)
mean_absolute_error(y_test, y_predict)

scikit-learn中没有提供RMSE

RMSE vs MAE

量纲相同
RMSE比MSE大
RMSE有放大y_hat与y较大差距的那个值的趋式
让RMSE更小的意义更大