问：求出第一主成分以后，如何求出下一主成分呢？

答：
第一步： 改变数据，将数据的第一个主成分去掉。

图中X'是X去除了第一主成分上的分量后的结果
第二步： 在新数据上求第一主成分

准备数据

import numpy as np
import matplotlib.pyplot as plt

X = np.empty((100, 2))
X[:,0] = np.random.uniform(0., 100, size=100)
X[:,1] = 0.75 * X[:, 0] + 3. + np.random.normal(0, 10., size=100)

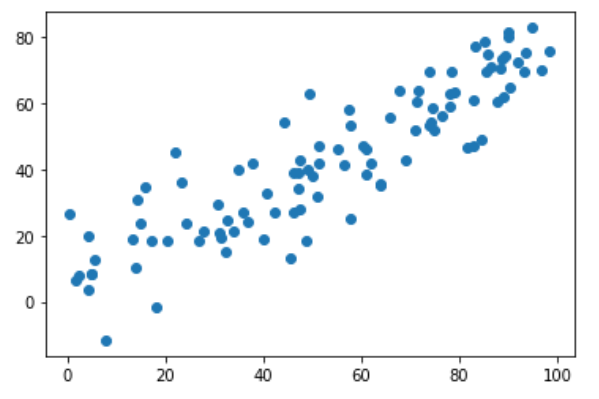
plt.scatter(X[:,0], X[:,1])
plt.show()

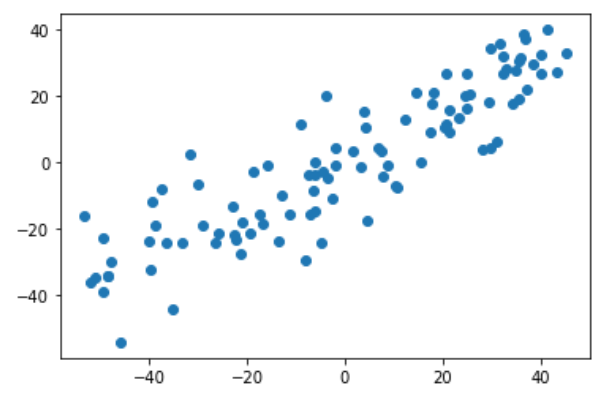
第一步：demean

def demean(X):
    return X - np.mean(X, axis=0)

X_demean = demean(X)
plt.scatter(X_demean[:,0], X_demean[:,1])
plt.show()

第二步：梯度上升法

def f(w, X):
    return np.sum((X.dot(w)**2)) / len(X)

def df(w, X):
    return X.T.dot(X.dot(w)) * 2. / len(X)

# 把向量单位化
def direction(w):
    return w / np.linalg.norm(w)

def first_component(X, initial_w, eta, n_iters=1e4, epsilon=1e-8):
    w = direction(initial_w)
    cur_iter = 0
    while cur_iter < n_iters:
        gradient = df(w, X)
        last_w = w
        w = w + eta * gradient
        w = direction(w)
        if(abs(f(w, X)) - abs(f(last_w, X)) < epsilon):
           break
        cur_iter += 1
    return w

训练和绘制结果

initial_w = np.random.random(X.shape[1])
eta = 0.001
w = first_component(X_demean, initial_w, eta)

输入：w
输出：array([0.77135006, 0.63641109])

第三步：去掉第一个主成分

方法一：

X2 = np.empty(X.shape)
for i in range(len(X)):
   X2[i] = X[i] - X[i].dot(w) * w

方法二：

X2 = X - X.dot(w).reshape(-1, 1) * w

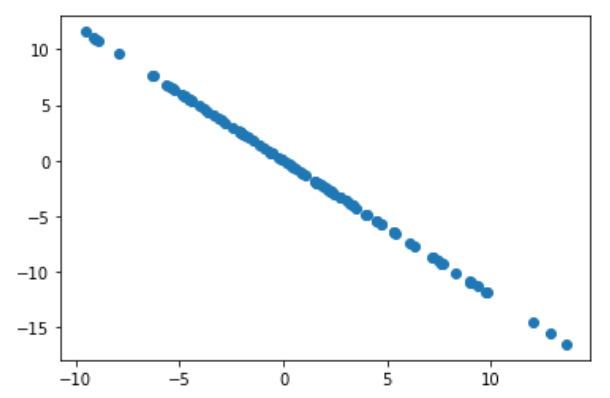
去掉第一主成分后的数据

plt.scatter(X2[:,0], X2[:,1])
plt.show()

第四步：求新数据的第一主成分

w2 = first_component(X2, initial_w, eta)

输入：w2
输出：array([-0.63639346, 0.77136461])

输入：w.dot(w2)
输出：2.2857453091384983e-05
点乘结果几乎为0，说明w和w2是垂直关系

封装成函数

def first_n_component(n, X, eta = 0.01, n_iters=1e4, epsilon=1e-8):
    X_pca = X.copy()
    X_pca = demean(X_pca)
    res = []
    for i in range(n):
        initial_w = np.random.random(X.shape[1])
        eta = 0.001
        w = first_component(X_pca, initial_w, eta)
        res.append(w)
        X_pca = X_pca - X_pca.dot(w).reshape(-1, 1) * w
    return res

输入：first_n_component(2, X)
输出：[array([0.77135082, 0.63641018]), array([ 0.63642749, -0.77133653])]
[?]遗留问题：我算出的第二个主成分的方向和视频中是反的？
可能是跟initial_w有关，多次运行后发现两个方向的结果都有。

LYBStudy