K(x, y)表示x和y的点乘。高斯核函数的公式为：

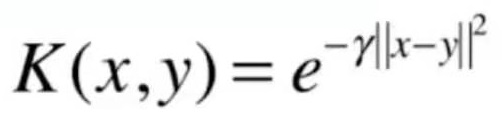
公式中的$$\gamma$$是高斯核函数中唯一的超参数。
高斯核函数 = RBF核 = Radial Basis Function Kernel = 镜像基函数
高斯核函数本质是将每个样本点映射到一个无穷维的特征空间

多项式特征为什么能处理线性不可分的问题？

依靠升维使得原本线性不可分的数据线性可分
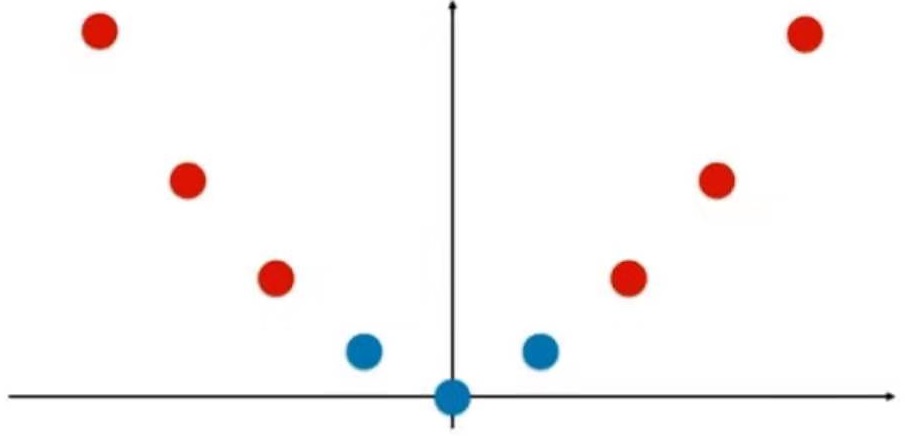
例如有一组原本线性不可分的一维数据：
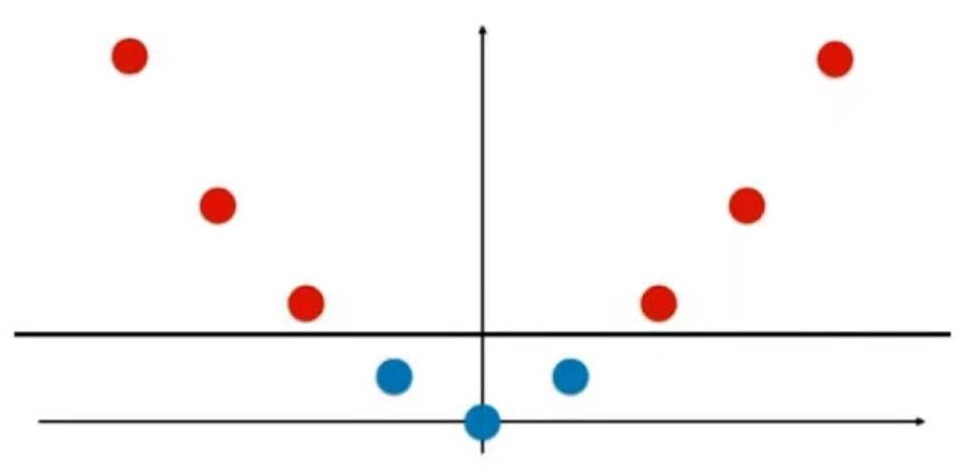
给数据增加一个内容为x^2的维度，数据就变成了这样： 现在很容易找到一根直线把两类数据区分开：

使用高斯核函数升维

再来看复用高斯核函数的例子。为了方便可视化，将原K做一些改变。
在原K中，是x相对y的映射，改成x相对两个固定的点的映射。
这两个固定的点就是图中的三角形位置。 l:landmark，地标

代码模拟高斯核函数的映射效果

import numpy as np
import matplotlib.pyplot as plt

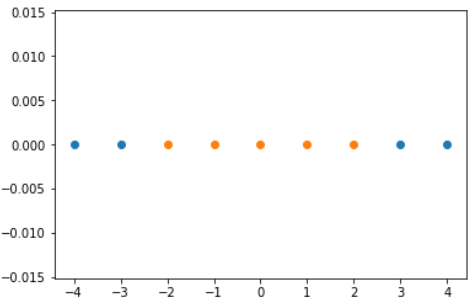
x = np.arange(-4, 5, 1)   # x = array([-4, -3, -2, -1,  0,  1,  2,  3,  4])
y = np.array((x>=-2) & (x<=2), dtype='int')   # y = array([0, 0, 1, 1, 1, 1, 1, 0, 0])

plt.scatter(x[y==0], [0]*len(x[y==0]))
plt.scatter(x[y==1], [0]*len(x[y==1]))
plt.show()

def gaussian(x, l):
    gamma = 1.0
    return np.exp(-gamma * (x-l)**2)

l1, l2 = -1, 1

X_new = np.empty((len(x),2))
for i, data in enumerate(x):
    X_new[i, 0] = gaussian(data, l1)
    X_new[i, 1] = gaussian(data, l2)

plt.scatter(X_new[y==0,0], X_new[y==0,1])
plt.scatter(X_new[y==1,0], X_new[y==1,1])
plt.show()

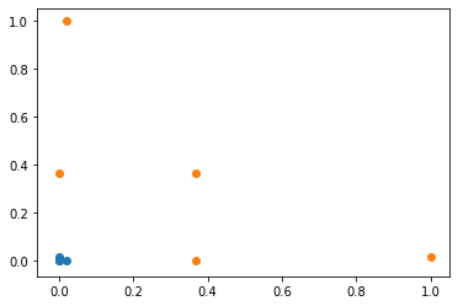
这样就得到了一个线性可分的结果：

解释

在这个例子中，使用图中的公式2来对x做映射，公式中的l1和l2是地标。
但实际的高斯公式是公式1，公式中的y是每一个数据点，也就是说，在高斯核函数中，每个样本都是一个地标landmark。它将m*n的数据映射成了m*m的数据。
使用高斯核函数训练样本，计算量非常大，训练时间也很长。
当m < n时，适用使用高斯核函数，例如自然语言处理。