P12
Diffusion Model 是如何运作的?
P13
Denoising diffusion models consist of two processes:
- Forward diffusion process that gradually adds noise to input
- Reverse denoising process that learns to generate data by denoising

P14
Forward Diffusion Process
The formal definition of the forward process in T steps:
直观理解

真正的加噪过程,不是直接的image + noise。
从数学上理解
✅ 从第一张图像到最后的纯噪声,实际上是分布的改变。
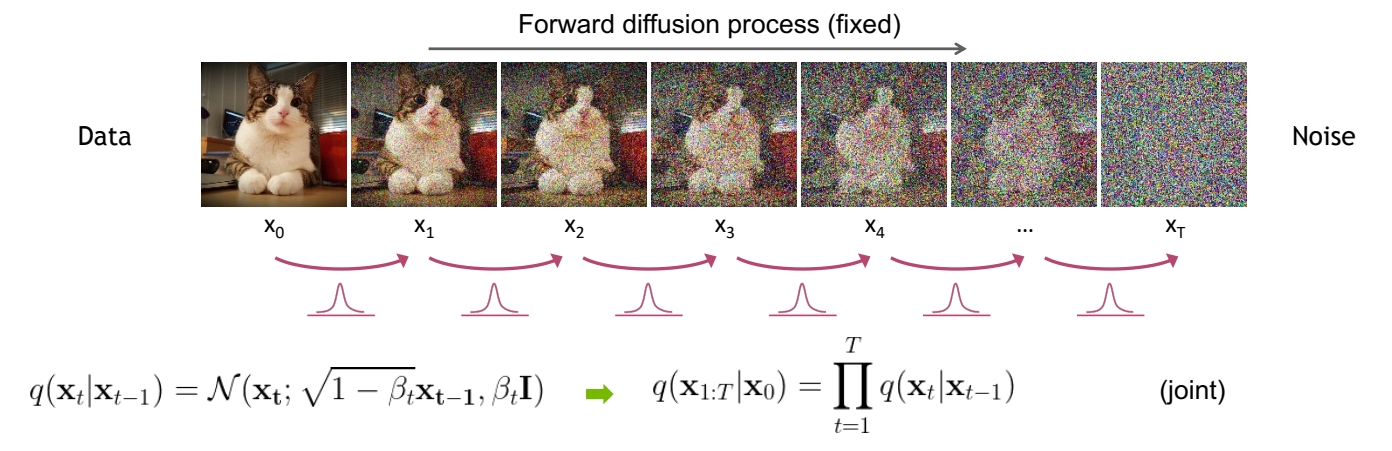
通过逐步的 scale down 让均值趋近于 0。通过引入噪声使方差趋近于 1。使得原始分布逐步逼近 \(\mathcal{N} (0,1 )\)分布,
❓ 求联合分布有什么用?
从操作层面理解

✅ 实际上,在给定一张图像x0时,想要获得第t张加噪图像时,不需要真的通过公式\(q(x_t|x_{t-1})\)从 \(\mathbf{x} _{t-1}\)到 \(\mathbf{x} _{t}\)一步一步计算出来,可以直接从 \(\mathbf{x}_0\)生成任意的 \(\mathbf{x}_t\)。
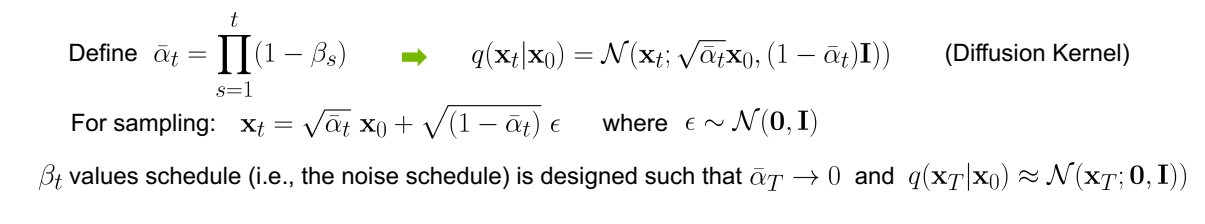
从数学上可以证明,从x0逐步计算到xt和从x0直接计算到xt,这两种行为是等价的。
根据公式 \(\mathbf{x} _t=\sqrt{\bar{a} _t} \mathbf{x} _0+\sqrt{(1-\bar{a} _t) } \varepsilon \)可知,当 \(\bar{a} _T → 0\),分布\(q(x_T)\)的均值趋于0,方差趋于1,变成纯高斯噪声。
P16
进一步理解
So far, we discussed the diffusion kernel \(q(\mathbf{x} _t|\mathbf{x} _0)\) but what about \(q(\mathbf{x}_t)\)?
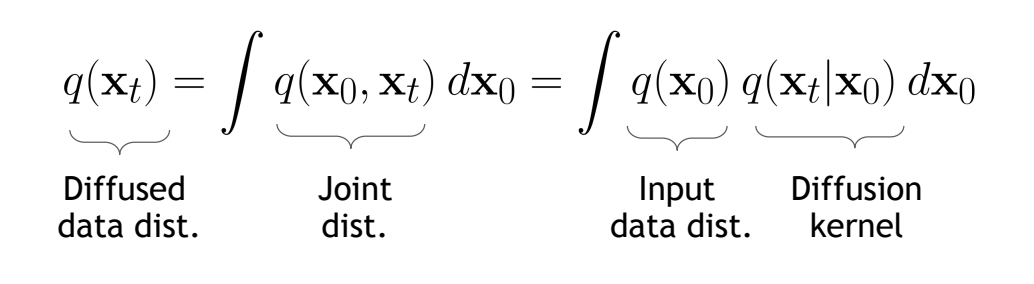
The diffusion kernel is Gaussian convolution.
✅ convolution 是一种信号平滑方法。
✅ \(q(\mathbf{x} _ t|\mathbf{x} _ 0)\) 是标准高斯分布,因此 \(q(\mathbf{x} _ t)\) 是以高斯分布为权重的真实数据的加权平均。
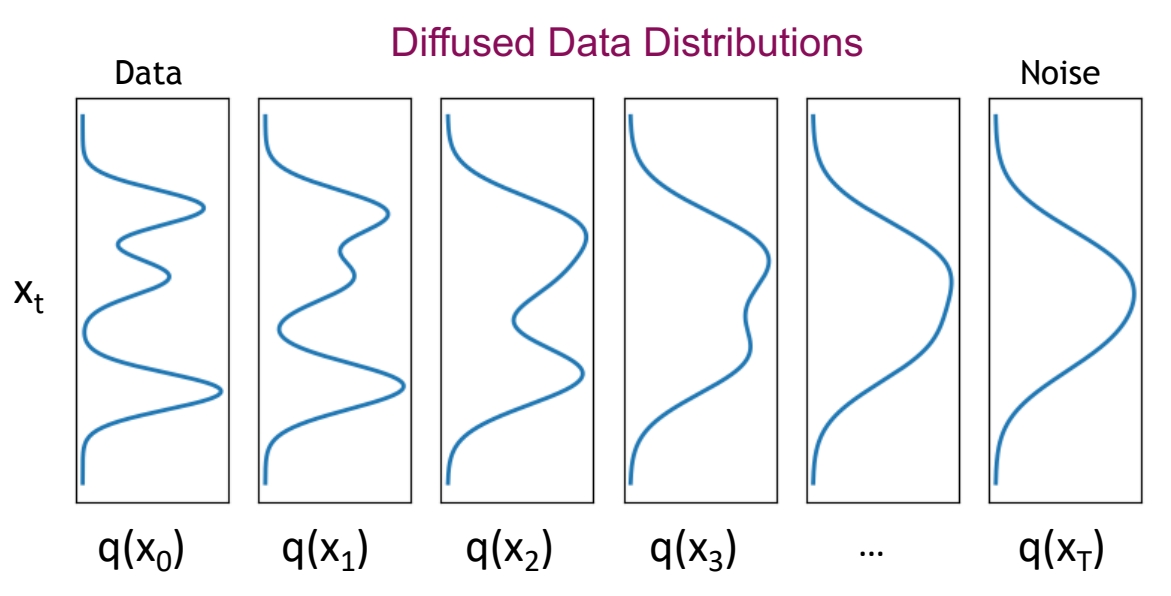
We can sample \(\mathbf{x}_t \sim q(\mathbf{x}_t)\) by first sampling \(\mathbf{x}_0\) and then sampling \(\mathbf{x}_t \sim q(\mathbf{x}_t|\mathbf{x}_0)\) (i.e., ancestral sampling).
✅ 实际上,没有任意一个时间步的 \(q(\mathbf{x})\) 的真实分布,只有这些分布的 sample.
Reverse Denoising Process
P17
直观理解
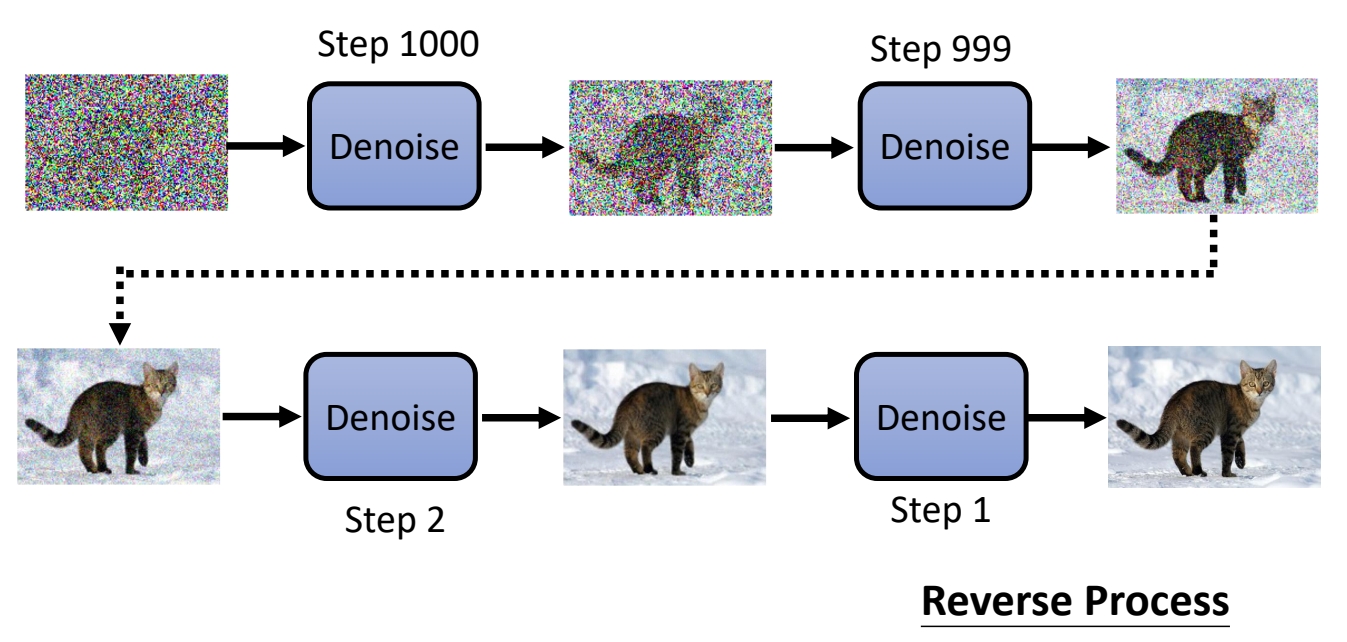

Denoise是一个网络模块,通过Denoise模块学习每个时间步的去噪过程。
✅ 把 \(\mathbf{x}_0\) 加噪为 init-noise,再从 init-noise 恢复出 \(\mathbf{x}_0\),这个操作是不可行的。
✅ 因为,根据公式 \(\mathbf{x} _t=\sqrt{\bar{a} _t} \mathbf{x} _0+\sqrt{(1-\bar{a} _t) } \varepsilon \), 且 \(\bar{a} _T → 0\),那么经过 \(T\) 步加噪后,\(\mathbf{x} _t\approx \varepsilon \). 而是 \(\varepsilon \) 是一个与 \(\mathbf{x} _ 0\) 没有任务关系的噪声,所以不可能从中恢复出 \(\mathbf{x} _ 0\).
从数学上理解
从xT到x0的过程,也是分布的改变。从\(\mathcal{N}(\mathbf{x}_T;\mathbf{0,I})\)w分布变成真实分布的过程。
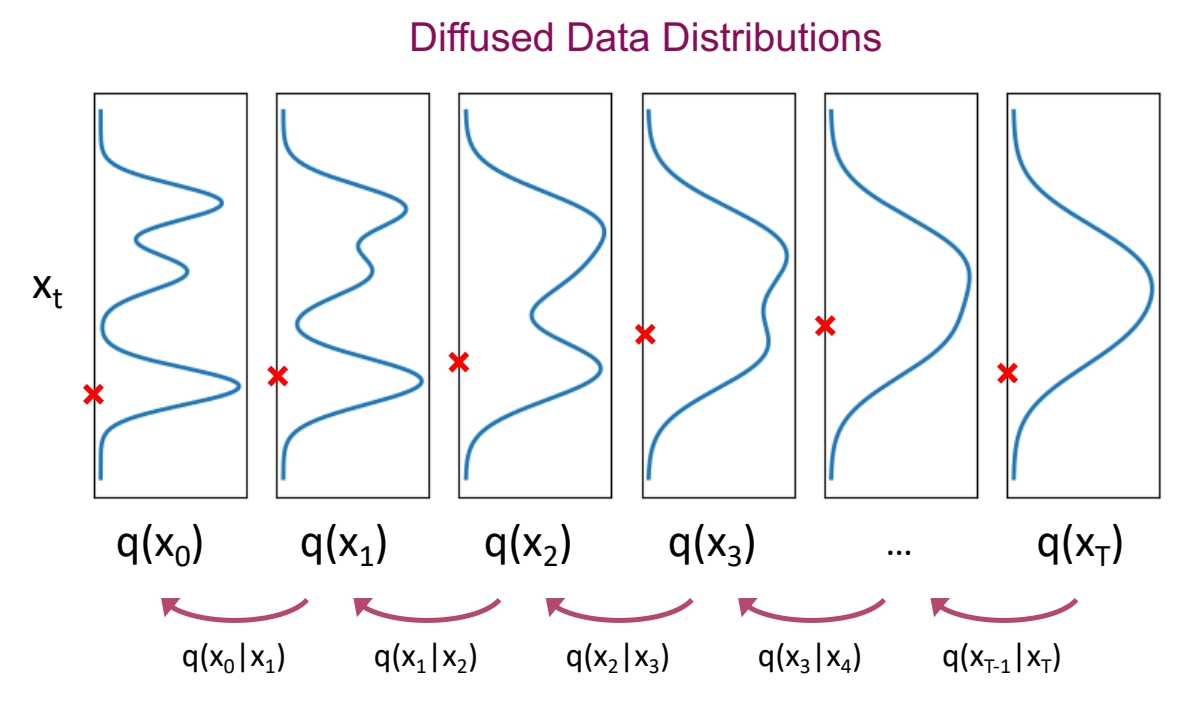

与Forward不同的是,\(q(\mathbf{x}_{t-1}|\mathbf{x}_t)\)没有一个准确的数学公式来表达。
Can we approximate \(q(\mathbf{x}_{t-1}|\mathbf{x}_t)\)? Yes, we can use a Normal distribution if \(\beta _t\) is small in each forward diffusion step.
✅ Nomal distribution 是特定均值和方差的高斯分布,不一定是 std 高斯。
P18
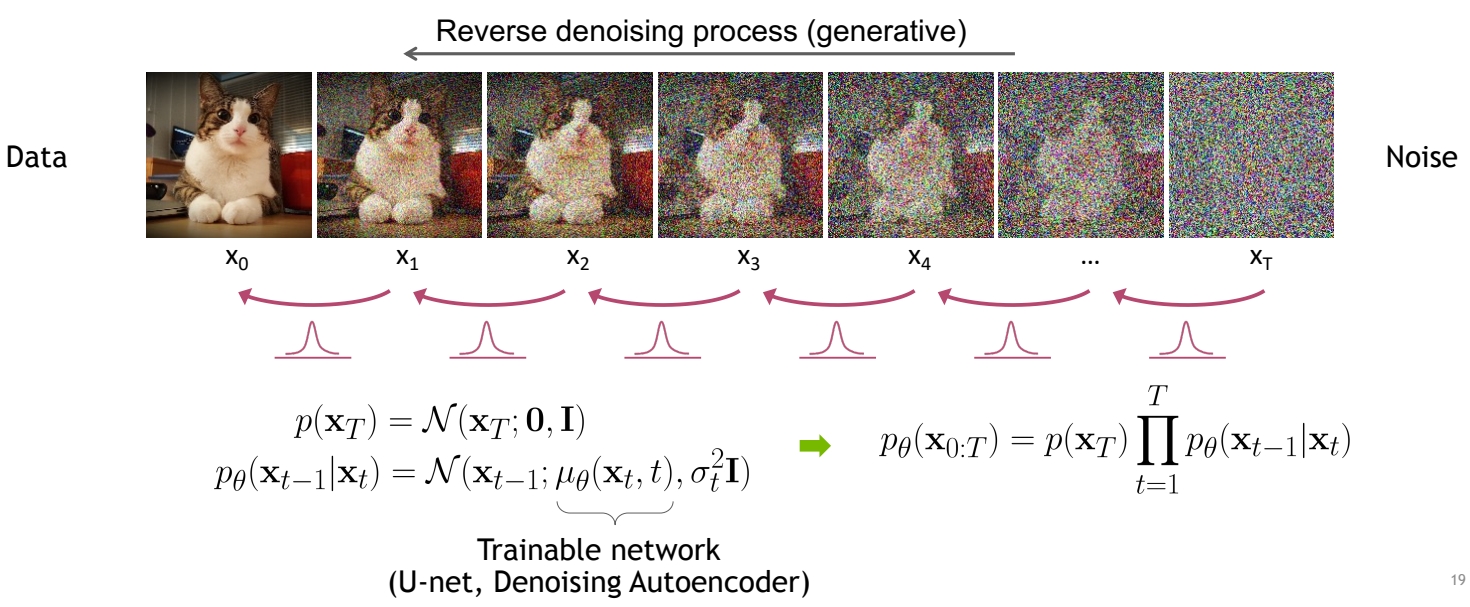
假设\(p(\mathbf{x} _ T)\)和\(p(\mathbf{x}_{t-1}|\mathbf{x}t)\)分别符合以上分布。
从第1个分布中sample出\(x_T\),把它代入第二个分布,就可以sample出\(x{T-1}\),直到最终sample出\(x_0\)
由于以上截图来自不同的材料,存在p和q混有的情况,需注意区分。
P19
Learning Denoising Model

✅ 以上是去噪模型的公式,下面有关于这些公式的详细解释。
P20
训练与推断
使用Forward流程对真实数据加噪,以构造pair data。
使用使用Denoise模块学习去噪分布,完成去噪过程。
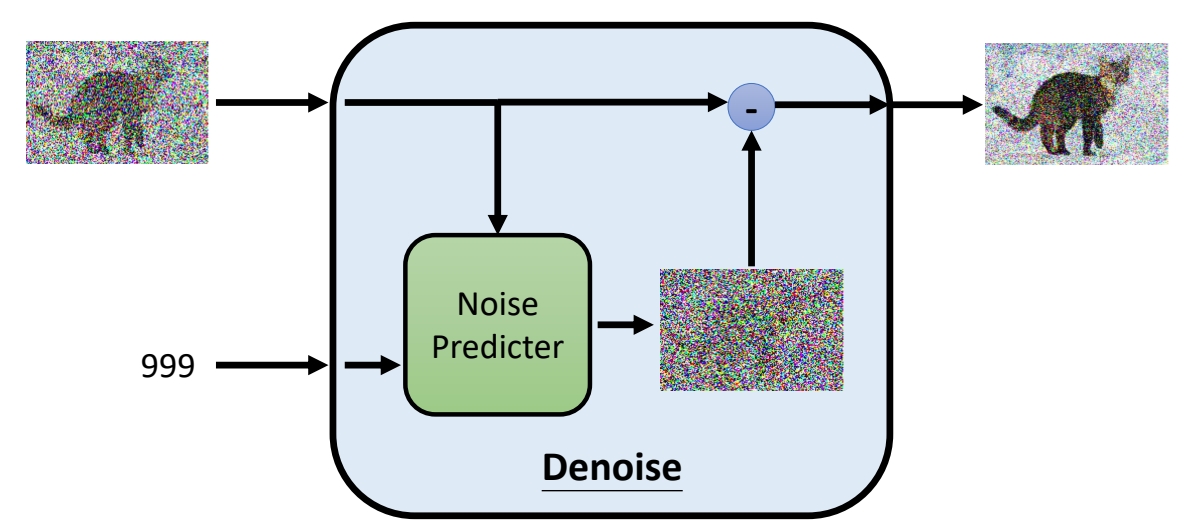

P21
Implementation Considerations
Diffusion models often use U-Net architectures with ResNet blocks and self-attention layers to represent \(\epsilon _\theta (\mathbf{x}_t,t)\).
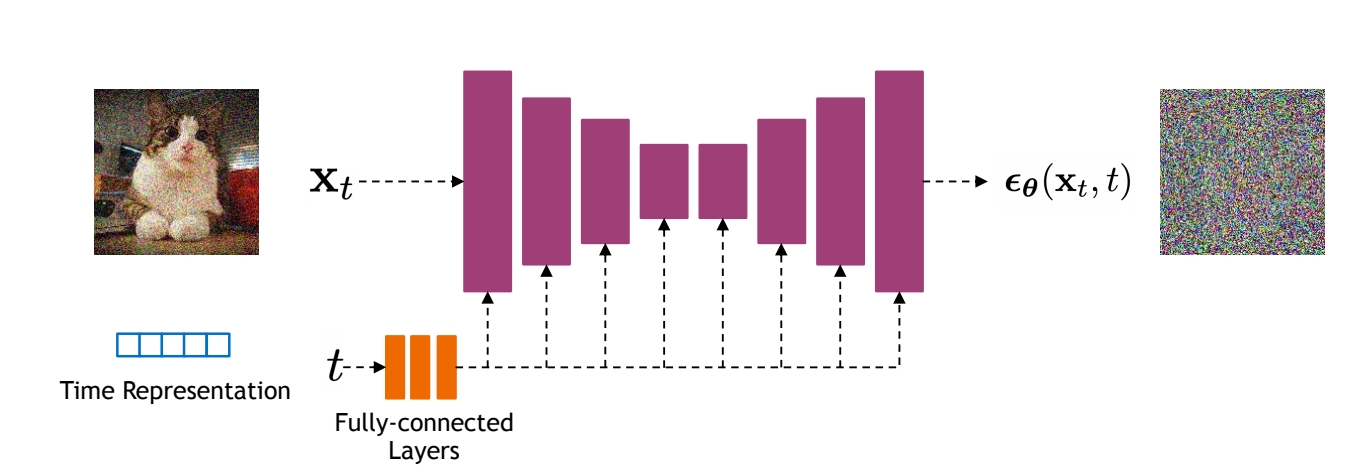
Time representation: sinusoidal positional embeddings or random Fourier features.
Time features are fed to the residual blocks using either simple spatial addition or using adaptive group normalization layers. (see Dharivwal and Nichol NeurIPS 2021).
✅ \(\sigma \) 是怎么定义的?
数学原理
P10
生成模型本质上的共同目标
目标是要学一个分布
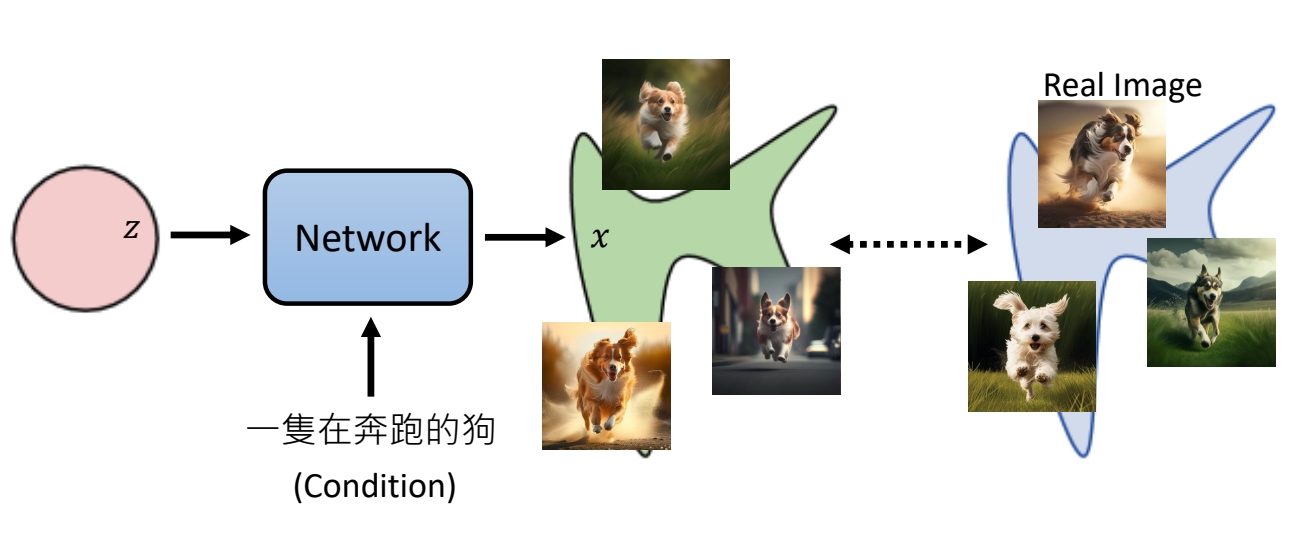
生成模型的本质是要学到真实数据的分布,以及从某个已经分布(通常是正态分布)到这个真实数据分布的映射。
✅ 实际使用中还会加一个 condition,但整体上没有本质差异,因此后面推导中不考虑 condition.
P11
定义目标函数
以Minimize KL Divergence作为目标函数
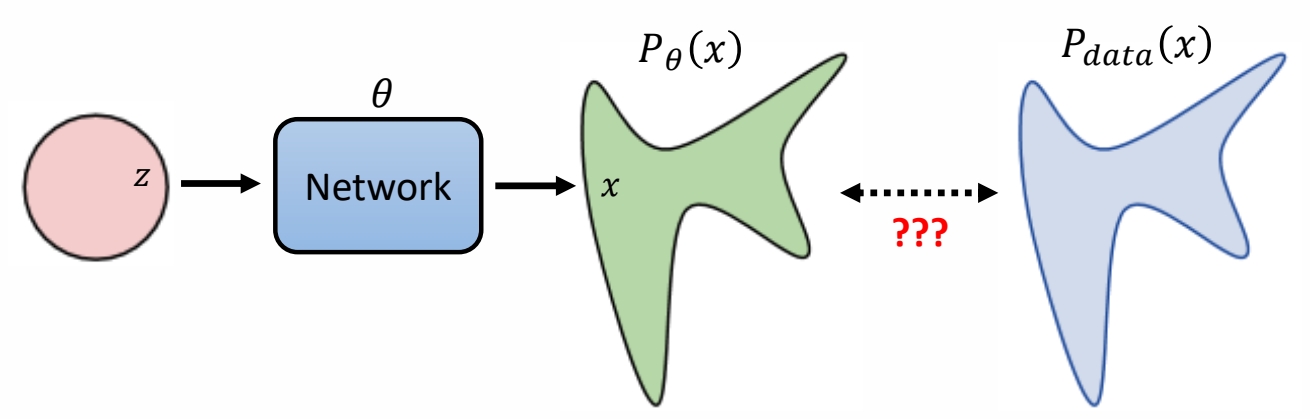
目标是让生成数据的分布与真实数据的分布尽量的接近,但是怎样衡量两个分布是否接近?
✅ 常用KL Divergence来衡量预测分布与GT分布之间的距离。
以Maximum Likelihood Estimation
\(P_{data}\) 代表真实分布,从分布中 Sample 出来的 \(x\) 即训练集
\(x_i\)是数据集里的一个数据,也是真实数据分布里的一个采样。\(P_\theta (x^i)\) 代表 \(P_\theta\) 生成 \(x^i\) 的概率。
✅ 由于 \(P_\theta\) 非常复杂,算不出这个概率,但此处假设 \(P_\theta (x^i)\) 已知。
于是可以将定义目标函数为:找出让真实 \(x^i\) 被生成出来的概率最高的\(\theta \).
\begin{align*} \theta ^\ast =\text{arg } \max_{\theta } \prod_{i=1}^{m} P_\theta (x^i) \end{align*}
两个目标函数是等价的
可通过数据推导证明,这里提到的两个目标,本质上是一致的。证明过程如下:
P12
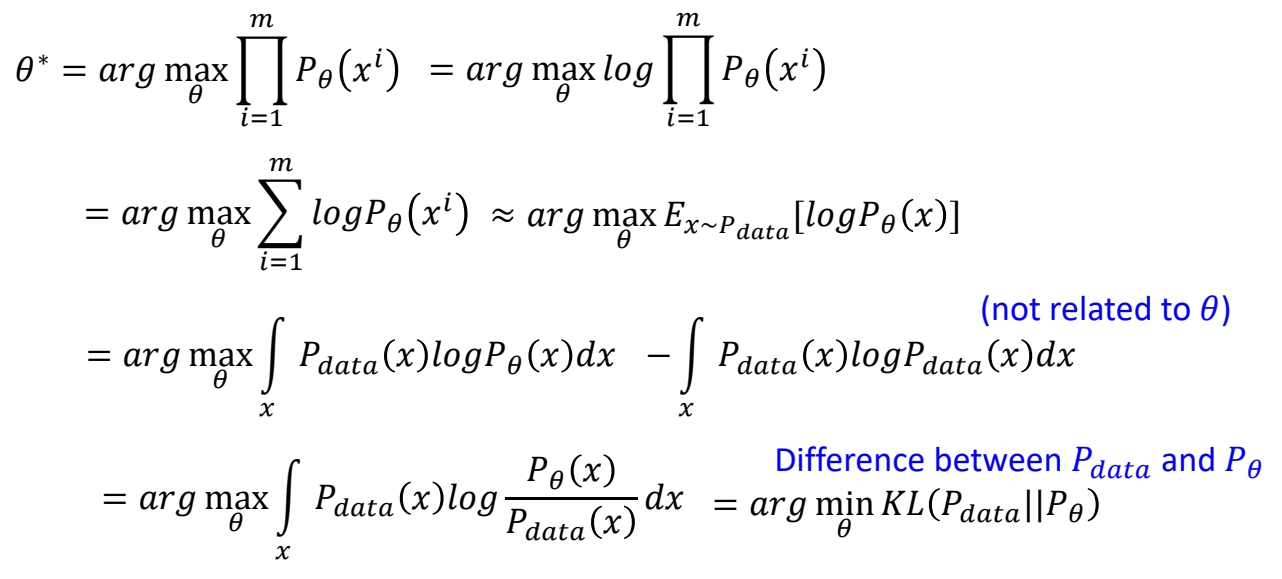
Maximum Likelihood = Minimize KL Divergence
✅ 结论:让真实数据的概率最大,与让两个分布尽量接近,在数学上是一致的。
✅ VAE、diffusion、flow based 等生成模型,都是以最大化 Likelihood 为目标。GAN 是最小化 JS Divergence 为目标。
P13
Compute \(𝑃_\theta(x)\)
计算\(𝑃_\theta(x)\)的常用技巧
✅ VAE 和 diffusion 非常相似,许多公式是通用的。
技巧一:不推断生成结果,而是推断生成结果分布的均值
 |  |
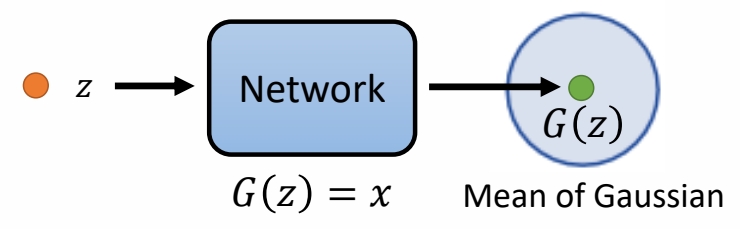 |  |
✅ \(G(z)\) 不代表某个生成结果,而是一个高斯的均值,然后计算 \(x\) 在这个分布中的概率。
P14
技巧二:不求\(𝑃_\theta(x)\),而是求Lower bound of \(log P(x)\)

✅ 通常无法最大化 \(P(x)\),而是最大化 \(log P(x)\) 的下界。
✅ 以上公式推导中省略参数 \( \theta\)。
P15
DDPM: Compute \(𝑃_\theta(x)\)
对于 diffusion model,假设每次 denoise 出的是一个高斯分布的均值。
❓ 问:为什么假设\(G(x_t)\) 是高斯分布的 mean?
✅ 答:有人尝试过其它假设,效果没有变好,且高斯分布便于计算。
通过链式法则,可以得出 \(x_0\) 在最终分布中的概率为:
$$
P_ \theta (x_0)=\int\limits _ {x_1:x_T}^{} P(x_T)P_ \theta (x_{T-1}|x_T) \dots P_ \theta (x_ {t-1}|x_t) \dots P_ \theta(x_0|x_1)dx_1:x_T
$$
P16
DDPM: Lower bound of \(log P(x)\)


计算Lower bound of \(log P(x)\)
计算\(q(x_t|x_{t-1})\)
P17
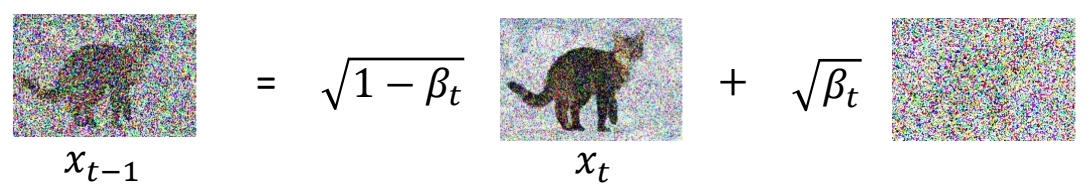
✅ 提前定好一组 \(\beta \).代表 noise 要加多大。
✅ \(q(x_t|x_{t-1})\) 仍然属于高斯分布,其均值为 \(\sqrt{1-\beta _t} \cdot x_t\),方差为 \(\beta _t\).
计算\(q(x_t|x_{0})\)
P18
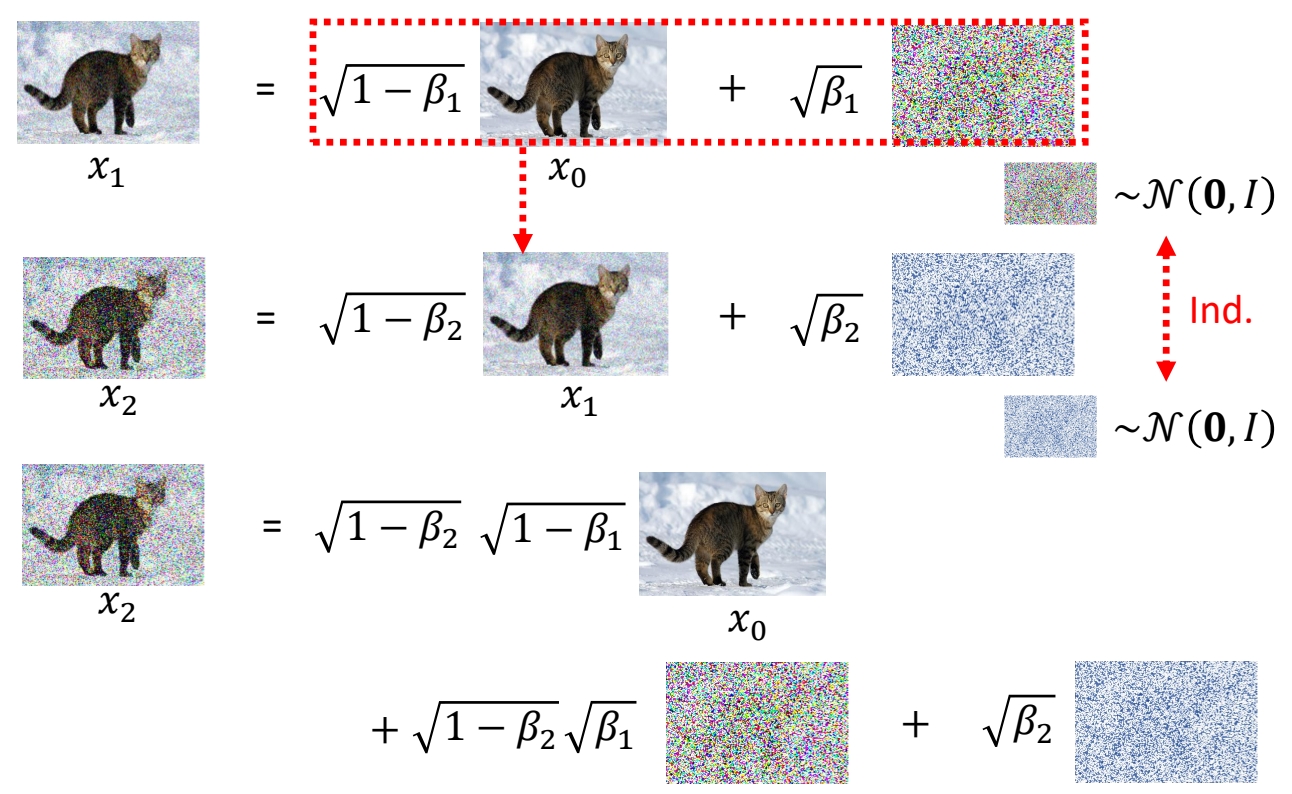
P19
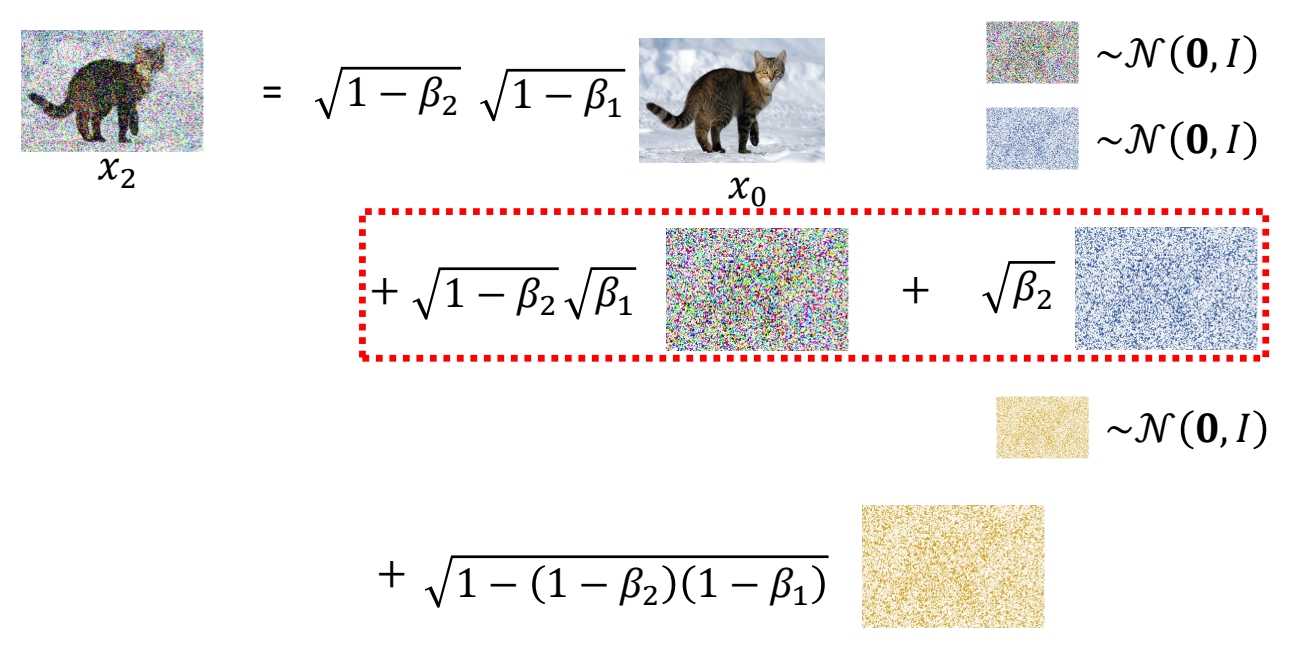
✅ 由于两次 sample 出的 noise 是独立同分布,两个 noise 以这种形式相加的结果,也符合某个特定的高斯分布。
P20

✅ 结论:\(q(x_t|x_{0})\)也符合高斯分布,其均值为\(\bar{\alpha }_t\),方差为\({1-\bar{\alpha }_t}\).
定义损失函数
如何定义损失函数,可以达到最大化\(\log P_{\theta}(x_0)\)的目的
损失函数与目标函数
目标函数是根据实际意义推导出来的优化目标。损失函数是能引导学习收敛到目标状态的函数,可以没有实际意义,也可以跟目标函数不一样。
虽然目标函数很明确,但是损失函数不一定要跟目标函数一样。可以从目标函数中提取出影响结果的关键因素来引导学习过程。
推导与简化目标函数\(log P(x)\)

P21
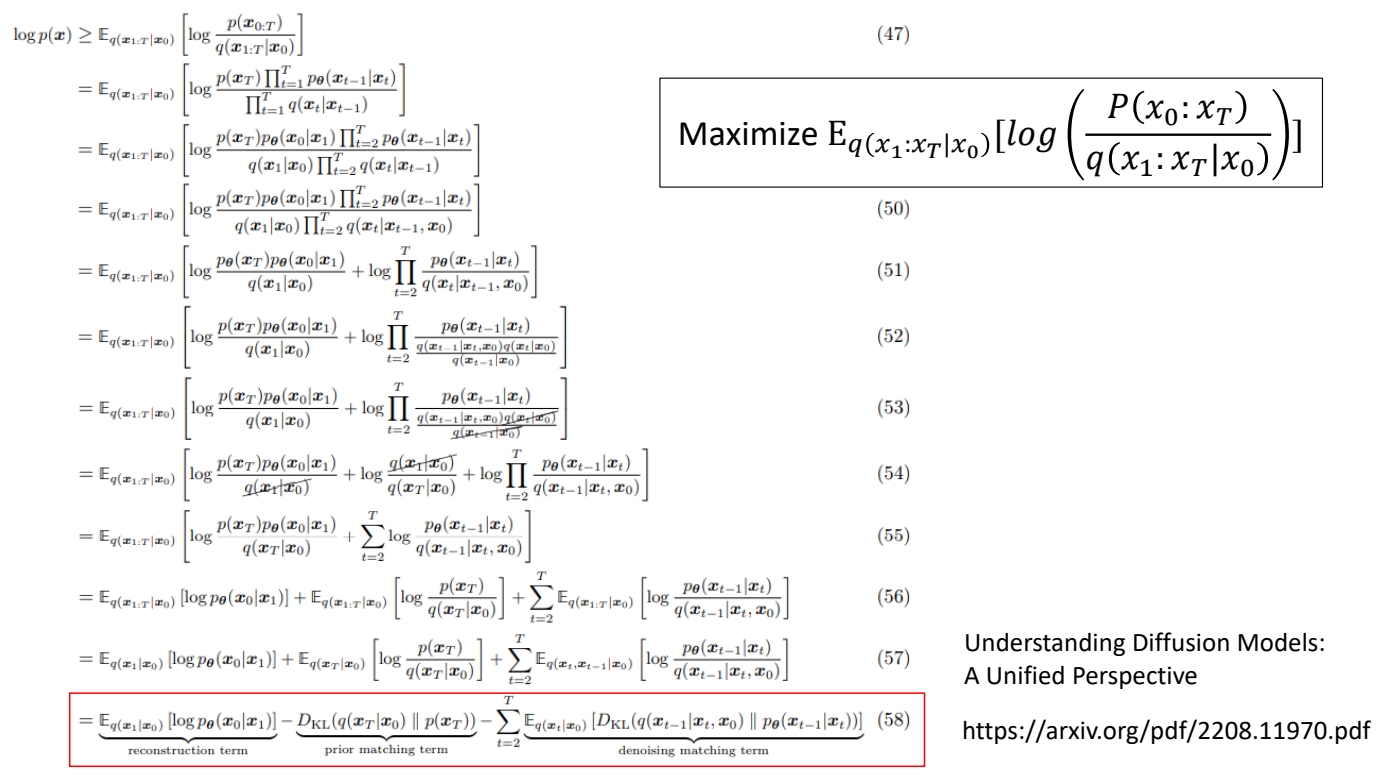
P22
最后简化为以下三项:
\begin{align*} E_{q(x_1|x_0)}[log P(x_0|x_1)]-KL(q(x_T|x_0)||P(x_T)) -\sum_{t=2}^{T}E_{q(x_t|x_0)}[KL(q(x_{t-1}|x_t,x_0)||P(x_{t-1}|x_t))] \end{align*}
分析目标函数中与优化相关的关键因素
结论
✅ 目标是要优化 \( \theta\),第二项与\( \theta\)无关,可以略掉。
✅ 第三项的 KL Divrgence 涉及到两个分布,分布1是固定的,可以通过计算得到,分布2是由 \( \theta\) 决定的,是要优化的对象。
P23
关于第三项分布1的推导过程

已知 \(q (x_t\mid x_0)\),\(q (x_{t-1} \mid x_0)\) 和 \(q (x_t \mid x_{t-1})\)为:
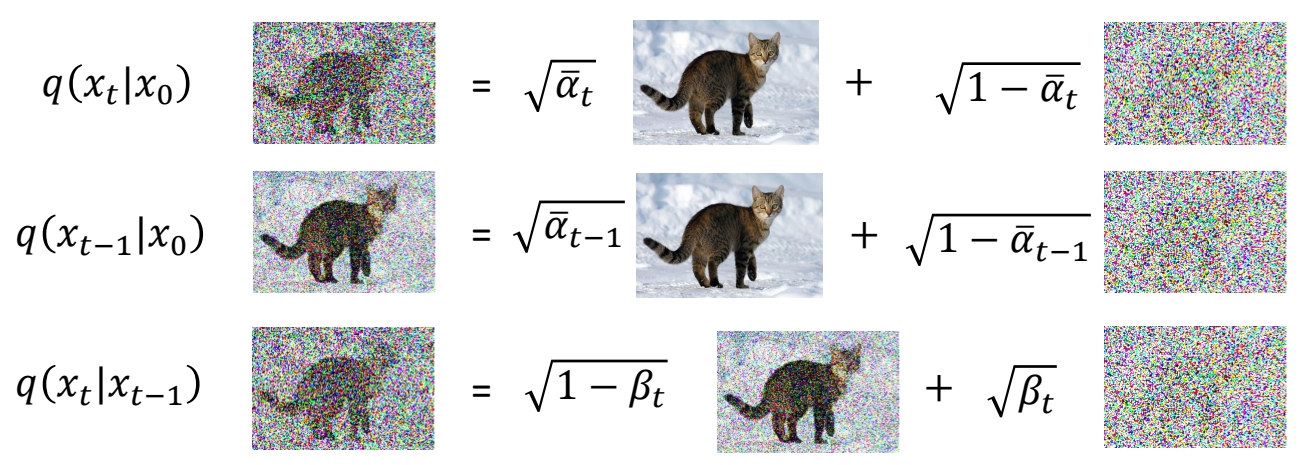
求 \(q (x_{t-1} \mid x_t,x_0)\).
✅ \((q(x_{t-1}|x_t,x_0)\)的数据含义为:已知\(x_0\) 和 \(x_t\),求 \(x_{t-1}\) 的分布。
P24

P25

https://arxiv.org/pdf/2208.11970.pdf
P26
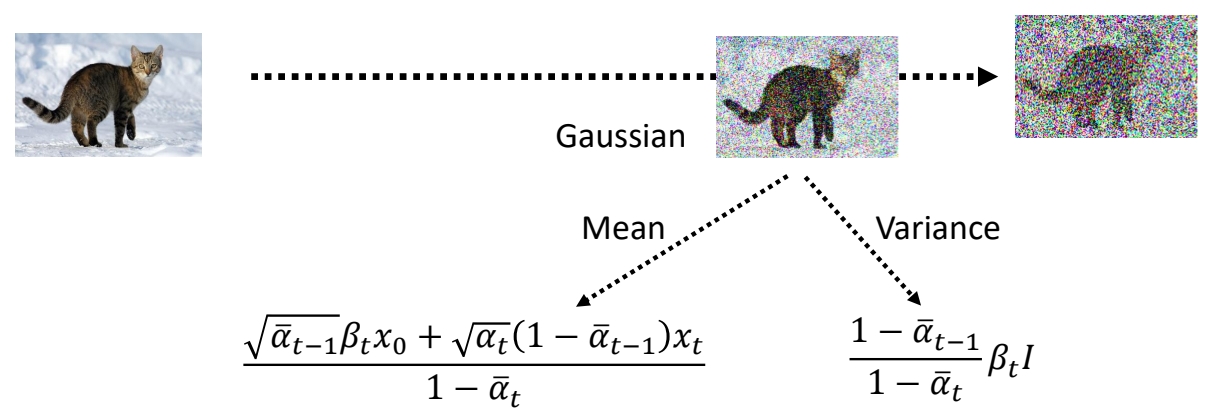
✅ 结论:\(q(x_{t-1}|x_t,x_0)\) 也是高斯分布,且其均值与方差是与\(\theta\)无关的固定的值。
化简后的目标函数
根据以上推导,目标函数可简化为最小化原目标函数第三项中分布1与分布2的KL Divergence。
\begin{align*} E_{q(x_1|x_0)}[log P(x_0|x_1)]-KL(q(x_T|x_0)||P(x_T)) -\sum_{t=2}^{T}E_{q(x_t|x_0)}[KL(q(x_{t-1}|x_t,x_0)||P(x_{t-1}|x_t))] \end{align*}
其中分布1为与\(\theta\)无关的固定,分布2为与\(\theta\)有关的待优化分布。
How to minimize KL divergence?
方式一:直接套公式

✅ 两个高斯分布的 KLD 有公式解,但此处不用公式解,因为 \( \theta\) 只能影响分布2的均值。
方式二
分布1的均值和方差是固定的。分布2的均值是待优化的,方差是固定的。
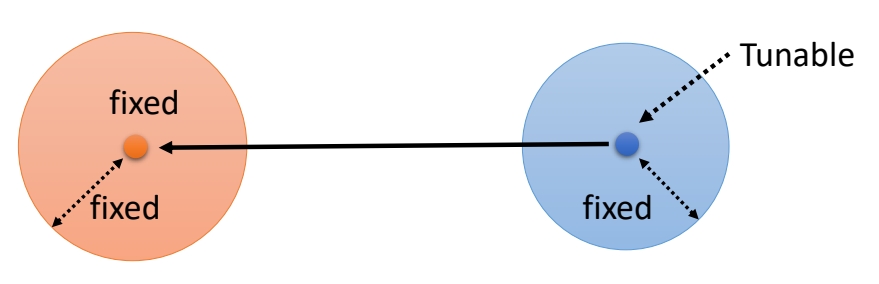
✅ 因此减小 KLD 的方法是让分布2的均值接近分布1的均值。
定义损失函数
✅ 分布1的均值可以看作是 \(x_{t-1}\) 的 GT 了。其计算公式为:
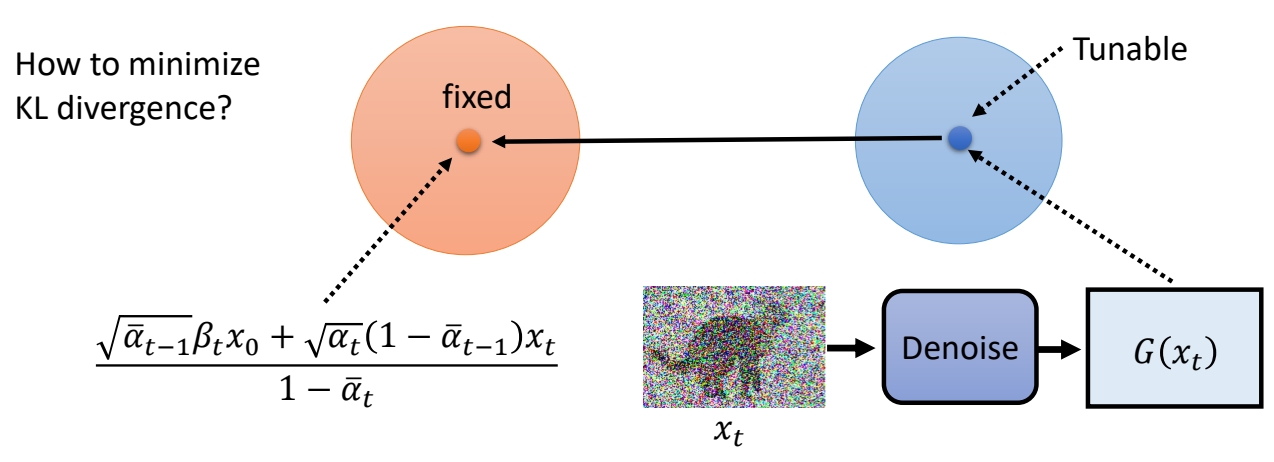
\(x_{t-1}\)的GT的计算公式中包含了x0和xt,把x0和xt都转化为xt的表示,得:
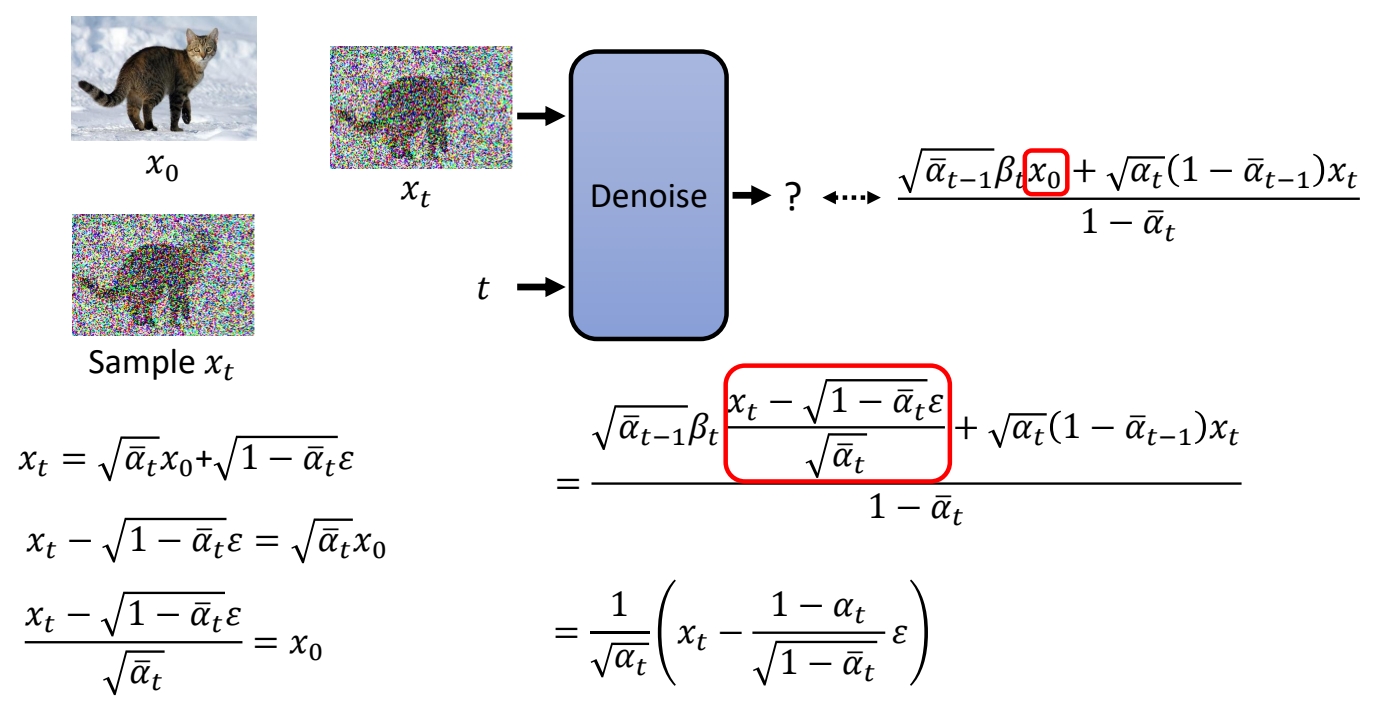
✅ 可以发现 \(x_t\) 与 \(x_{t-1}\)和GT 之间,唯一未知的部分就是 noise \(\varepsilon \). 因此用网络学习这个noise。
最终定义损失函数为网络输出(预测的noise)与GT(构造训练数据时所生成的noise)之间的L2距离。
其它问题
关于\(\alpha \)
✅ \(\alpha \) 是预定义的超参,DDPM 试图学习 \(\alpha \),发现没有提升。
相关论文
| ID | Year | Name | Note | Tags | Link |
|---|---|---|---|---|---|
| 2015 | Deep Unsupervised Learning using Nonequilibrium Thermodynamics | ||||
| 2020 | Denoising Diffusion Probabilistic Models |
本文出自CaterpillarStudyGroup,转载请注明出处。
https://caterpillarstudygroup.github.io/ImportantArticles/