The Generative Modeling Problem
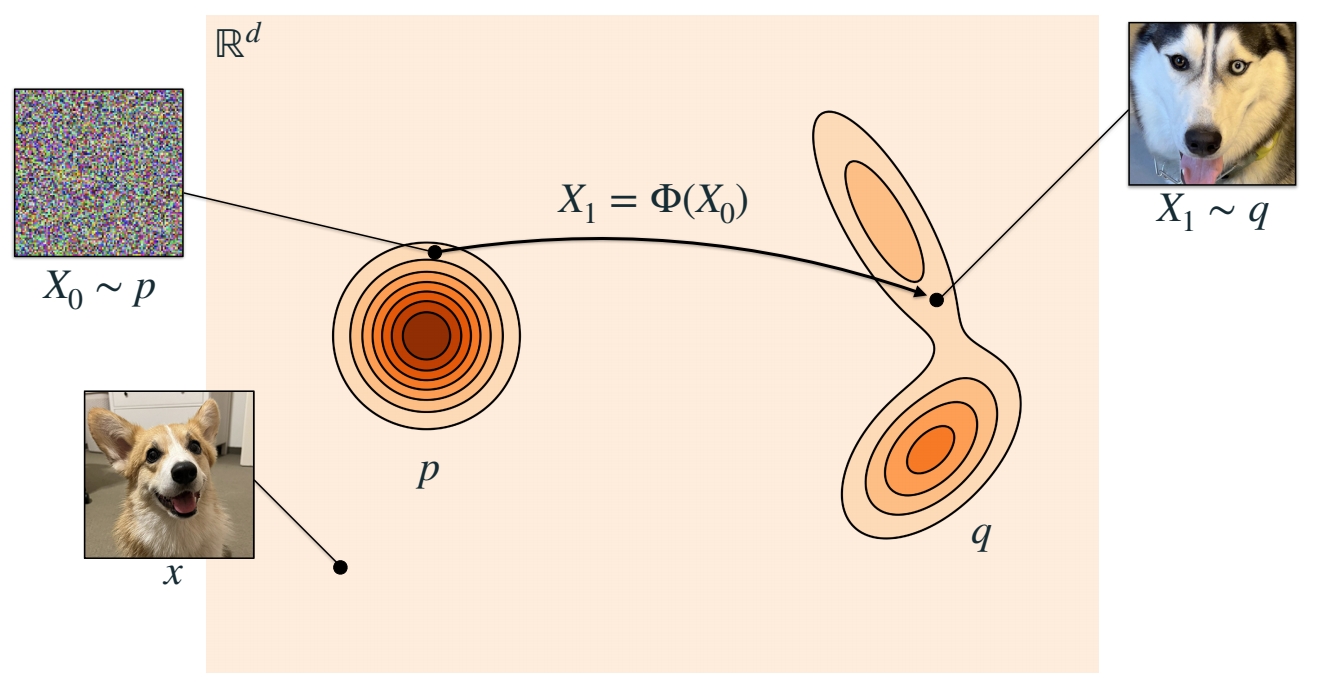
正方形代表所有可能的状态所构成的空间,即图像空间。正方形中的每个点代表一个sample,即一张图像。
\(P\) 是源分布,\(Q\) 是目标分布。
\(X_0\) 和 \(X_1\)分别是 \(P\) 分布和 \(Q\) 分布中的 sample.
生成模型的目标是,找到一个可以从 \(P\) 中 sample 到 \(Q\) 中 sample 的映射。
P9
生成模型的范式
生成模型有两大类范式:直接生成和增量生成。
直接生成
GAN、VAE 属于第一大类生成模型,优点是快,因为它的生成过程只需要一个forward。
GAN的缺点是:
(1)没有一个精确的可以用于 sample 的概率模型
(2)难以训练。
自回归 VS 非自回归
要生成的内容是一个整体,可以一次性生成整个内容,也可以把要生成的内容分解成多个小块,分别生成这些小块,再合成整体。
例如图像生成,PixelCNN、ViT把图像分成多个patch,并分别生成这些patch。为了让这些patch之间有协调性,后生成的patch要以已生成的patch为依据。
再例如动作生成,要生成一个动作序列,可以把每一帧作为一个patch,也可以把连续的几帧作为一个patch。
自回归生成的特点是,生成内容的依赖关系是固定的。先生成的patch会对后生成的patch产生影响,反之则不行。
增量生成
增量生成是另一种生成范式,不是直接生成最终结果,而是逐步生成。每一次生成比上一次要好。
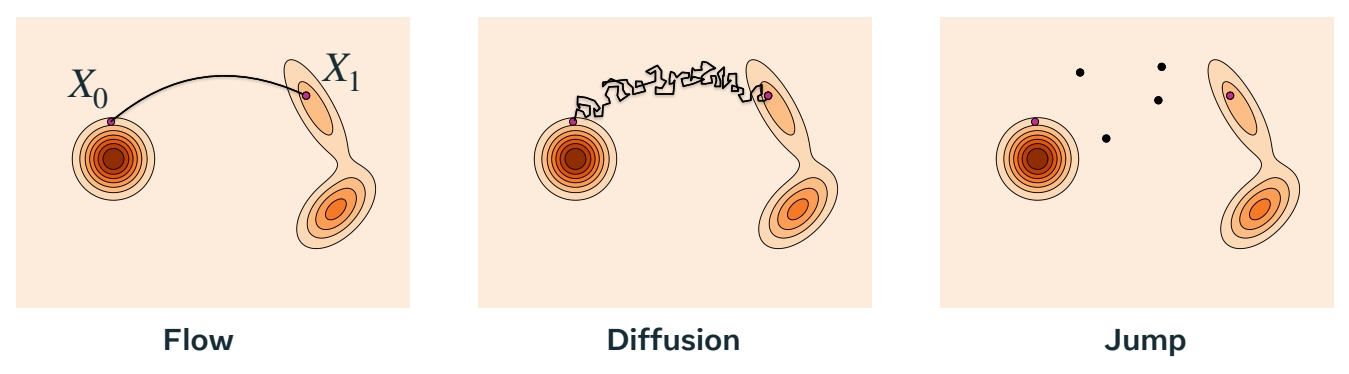
| 生成模型 | 特点 | 链接 |
|---|---|---|
| Flow Matching | 转移过程是平滑的。 | link |
| Diffusion | 转移过程是连续但不平滑的 | link |
| Jump | 转移过程是不连续的 | |
| Score Matching | link | |
| DSDFM | std normal --(flow matching/score matching)--> VQ-VAE latent --(VQ-VAE)--> pixel | link |
共同点:都是基于连续时间马尔可夫过程的随机过程Continuous-time Markov process。
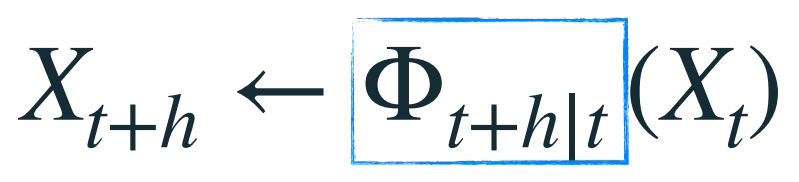
\(\Phi\) 是从一次生成到另一次生成的转移函数。
增量生成模型的目标是学习转移函数。