P34
Flow Matching Advanced Designs
P35

1.条件生成
2.\(P\) 分布和 \(Q\) 分布耦合的场景
3.在几何域上使用 flow matching 构造生成模型
P37
Conditioning and Guidance
问题定义:
数据集:样本 + 标签
生成:给定标签,从具有特标签的分布中采样
P39
Conditional Models
公式定义
$$ p_ {t,1|Y} (x, x_1|y) = p_ {t|1}(x|x_1)q(x_1|y) $$
| 无条件 | 条件 |
边缘概率分布 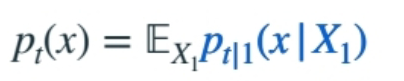 | 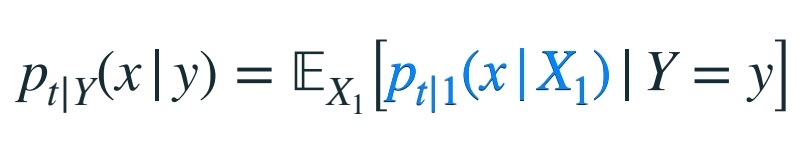 |
边缘速度 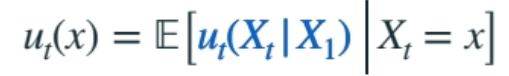 | 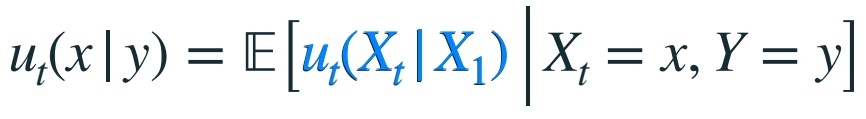 |
将条件概率路径构建为不显式依赖于条件 \(Y\)。
P40
网络训练
Train same neural network on all conditions:

对于网络训练的影响在于,数据增加一个维度来表示\(Y\)。
P41
Examples

🔎 “Flow Matching for Generative Modeling” Lipman et al. (2022)
🔎 “GLIDE: Towards Photorealistic Image Generation and Editing with Text-Guided Diffusion Models” Nichol et al. (2021)
局限性
此方法在“每个条件都有大量数据”时很有用,例如条件是类别时。
条件是文本时不适用,因为数据集里一段文本通常只对应一张图像。
P42
Condition as Guidance
Score Matching 和 diffusion
classifier Guidance:通过引入分类器,将无条件模型变成条件模型.
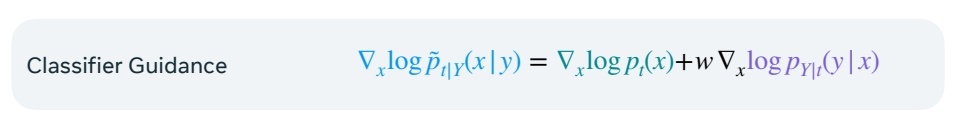
CFG:条件生成结果与无条件生成结果外插。
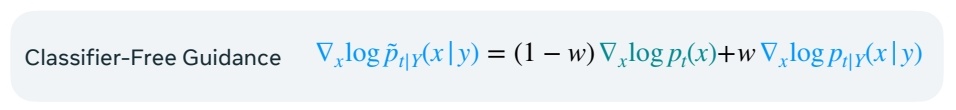
🔎 CFG
P43
Flow Matching with Caussian Path
Assume a velocity field trained with Gaussian paths.以上来自 score matching 的公式,同样可以适配到 flow matching.
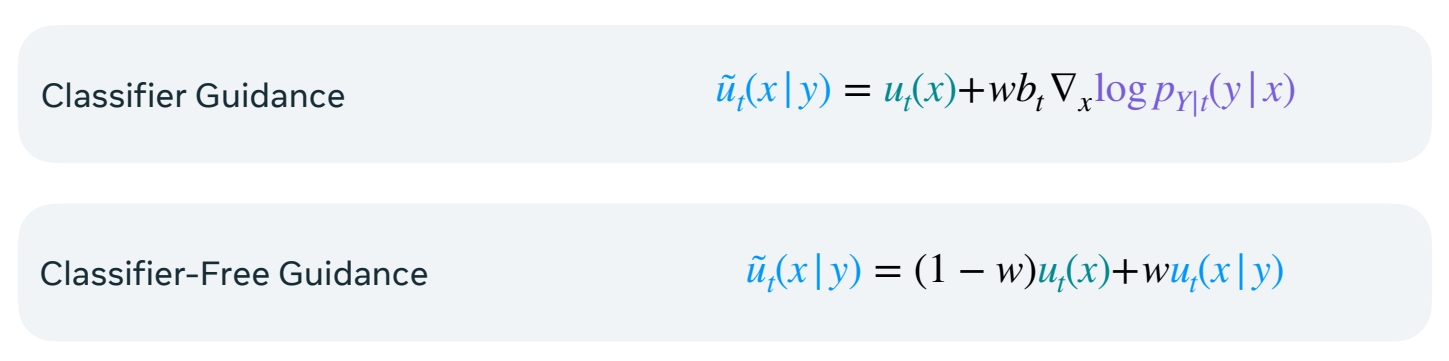
P44
相关工作:
🔎 "Guided Flows for Generative Modeling and Decision Making" Zheng et al. (2023)
🔎 "Mosaic-SDF for 3D Generative Models" Yariv et al. (2023)
🔎 "Audiobox: Unified Audio Generation with Natural Language Prompts" Vyas et al. (2023)
🔎 "Scaling Rectified Flow Transformers for High-Resolution Image Synthesis" Esser et al. (2024)
🔎 "Movie Gen: A Cast of Media Foundation Models" Polyak et al. (2024)
P45
其中,movie Gen 发现使用 flow matching loss,在生成质量和文本一致性上,均优于 diffusion loss.
P46
非 Gaussian Path
Open Problem
How to guide FM with non-Gaussian paths?
CFG 要求正在学习的是具有高斯路径的 flow matching 模型,但 flow matching 不局限于高斯源。
P52
Data Couplings
前面工作都假设 \(P\) 和 \(Q\) 是独立的。What about dependent couplings?
 |  |
| • Non-Gaussian source distribution • Alternative conditioning approach • Inverse problems | • Applications to Optimal Transport • Efficiency: straighter trajectories |
两种方法,利用 \(P\) 和 \(Q\) 的耦合关系优化生成过程。
1.利用耦合关系,构造另一种条件方法,用于解决 Inverse 问题。
2.试图找到多样本之间的耦合关系,用于优化采样效率。
P58
Paired Data
问题定义

方法
Alter source distribution and coupling instead of adding condition
改变源分布和耦合,而不是添加条件。
从数据中取出样本\((X_1,Y)\)
[❓] \(X_1\) 和 Y 有什么区别?
根据Y构造\(X_0\)
$$ X_0=Y+\epsilon \sim p $$
源分布不是噪声,而是 \(Y\) 添加噪声,损失不变。
P61
Result
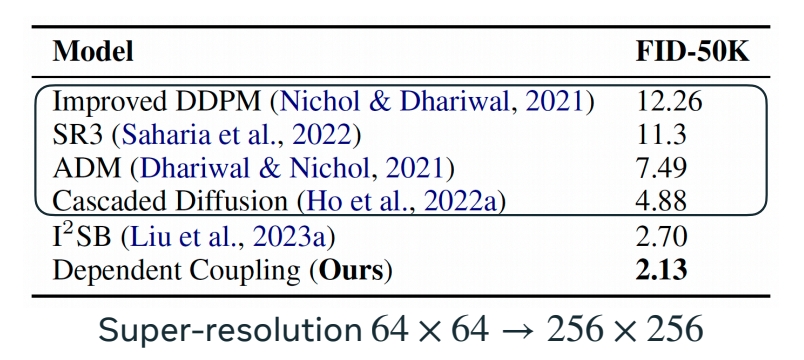
P63
Multisample Couplings
问题定义
Given uncoupled source and target distributions,can we build a coupling to induce straighter paths?
有一个预训练的 flow matching 模型,构建一种耦合,使 \(P\) 到 \(Q\) 的路径更直线,或 \(Q\) 能更好地采样。

P64
耦合的本质
耦合 cost 限制了动能.降低 coupling cost,就能减少动能。
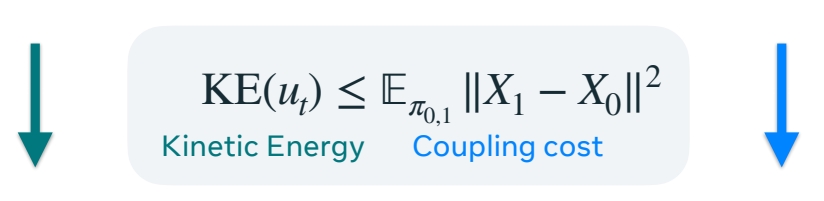
对于不同的耦合关系会得到不同的 \(u_t\) 和动能。但它有上限,降低上限能减少动能。
Marginal \(u_t\) with cond-OT FM and \(π_{0,1}\)
P69
方法
Use mini batch optimal transport couplings

- 从 \(P\) 分布和 \(Q\) 分布中随机采样 \(k\) 个点。
- 寻找两组点之间的最优排列,来最小化 cost.
- 假设找到了最优组合,随机选择一对。
P70
$$
\mathrm{When} \quad k = 1 → π_{0,1} = p(X_0)q(X_1)
$$
当 \(k=1\) 时,相当于 \(P\) 和 \(Q\) 是独立的。
P71
When \(k → ∞, u_t\) generates the Optimal Transport map
P72
Result
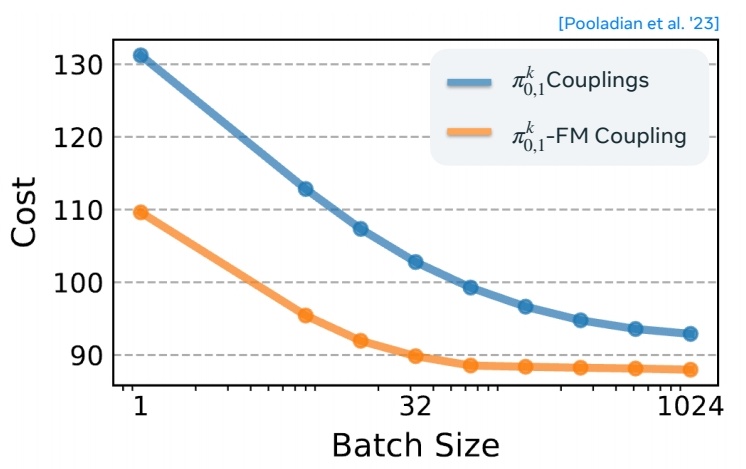
- High dimensions-minor improvement in sampling speed compared to tailored samplers.
低维时,此方法能明显降低 cost
- Shows promise in lower dimensional problems for scientific applications (e.g. protein backbone design [Bose et al.'23]).
高维时,路径本身已接近直线,因此效果不明显。
P73
相关工作
Paired data:
🔎 "I2SB: Image-to-Image Schrödinger Bridge" Liu et al. (2023)
🔎 "Stochastic interpolants with data-dependent couplings" Albergo et al. (2024)
🔎 "Simulation-Free Training of Neural ODEs on Paired Data" Kim et al. (2024)
Multisample couplings:
🔎 "Multisample Flow Matching: Straightening Flows with Minibatch Couplings" Pooladian et al. (2023)
🔎 "Improving and generalizing flow-based generative models with minibatch optimal transport" Tong et al. (2023)
🔎 "SE(3)-Stochastic Flow Matching for Protein Backbone Generation" Bose et al. (2023)
🔎 "Sequence-Augmented SE(3)-Flow Matching For Conditional Protein Backbone Generation" Huguet et al. (2024)
🔎 "Flow Straight and Fast: Learning to Generate and Transfer Data with Rectified Flow" Liu et al. (2022)
P75
Geometric Flow Matching
使用 Flow Matching 生成(对称的或黎曼流型的)几何
| Data with Symmetries | Riemannian Manifolds |
 |  |
| • Equivariant flows → invariant densities • Alignment couplings | • Simulation free on simple manifolds • General geometries |
P87
Data with Symmetries
问题定义
有些对象具有对称性,希望生成的对象也能满足这些特征。
对称性的直观理解和公式表示
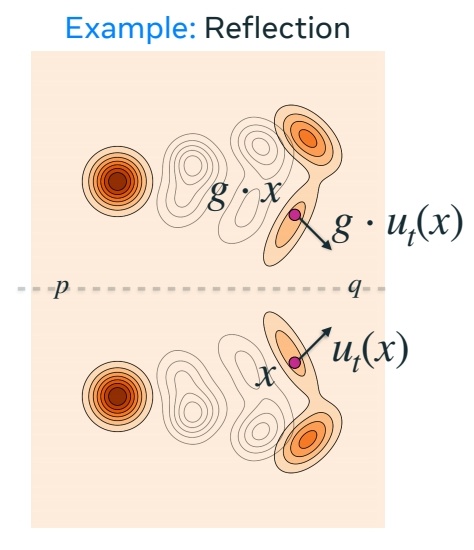
原始 \(P、Q\) 分布与对称 \(P、Q\) 分布应具有相同的密度或似然性。
边缘概率路径也应具有对称性,且原概率路径保持不变。
$$ p_t(g\cdot x)=p_t(x) $$
等变性:是教学中关于的群的术语,在这里简单理解为具有对称性。
边缘概率路径具有对称性和边缘速度具有对称性,是等价的。
等变速度场可以生成不变的概率路径和等变流。

🔎 "Equivariant Flows: Exact Likelihood Generative Learning for Symmetric Densities" Köhler et al. (2020)
P88
方法
因此,只需要构建一个能生成等变速度的 flow matching model。
Equivariant Velocity
$$ u^θ_t (g⋅x) = g⋅u^θ_t(x) $$
Train with CFM:

🔎 "Equivariant flow matching" Klein et al. (2023)
🔎 "Equivariant Flow Matching with Hybrid Probability Transport" Song et al. (2023)
P89
存在的问题
数据是具有对称性的。
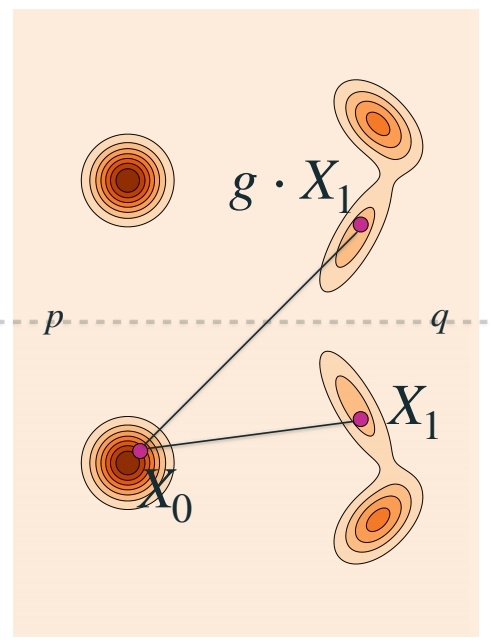
如果没有考虑数据的对称性,仍假设 \(P\) 和 \(Q\) 是独立的,会发生这种情况。
P90
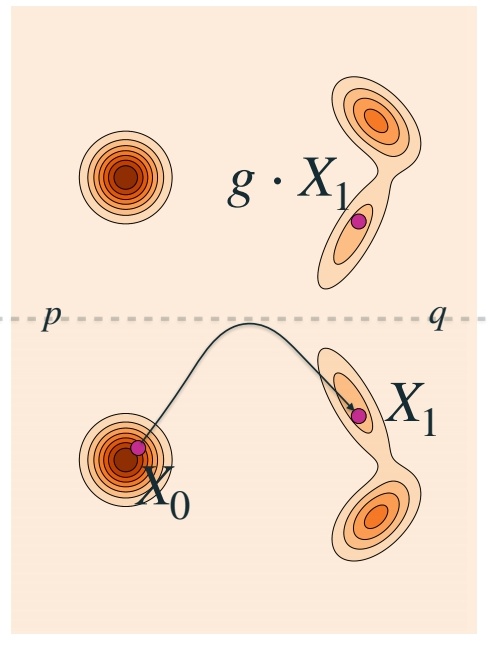
导致模型学到的轨迹弯曲。降低 sample 的效率。
P91
解决方法
🔎 "Equivariant flow matching" Klein et al. (2023)
🔎 "Equivariant Flow Matching with Hybrid Probability Transport" Song et al. (2023)
这两篇 Paper 提出对齐耦合;解决以上问题。
P92
Result
| "Fast Point Cloud Generation with Straight Flows" Wu et al. (2022) | "Equivariant Flow Matching with Hybrid Probability Transport" Song et al. (2023) "Equivariant flow matching" Klein et al. (2023) |
 |  |
此方法适用于点云和分子。
P94
Generative Modeling on Manifolds
生成流形数据,例如 Nesh,轨迹、曲面等而不是整个欧拉空间。
P95
Need to re-define the geometric structures we have in Euclidean space.
重新定义几何结构,以便定义 flow matching 模型。
此处以黎曼流形为例。
P98
定义几何结构
🔎 黎曼流形
假设只考虑黎曼流形
1.光滑流形,即可微,能够定义切空间。
切空间是某点\(x\)处所有方向导数的集合。
2.选择一个内积来计算黎曼度量,描述流形上的角度和距离。
P99

Pl00
构建黎曼流形时,速度定义在切空间上。
这样速度 \(v\) 和流形 \(x\) 不在同一空间,计算出 \(v\) 以后,要投影回 \(x\),转成流形。
P101
构建 Riemannian Flow Matching
图像上的 flow matching 与黎曼空间上的 flow matching,具有相同的数据构造、训练方法、唯一的不同是 Loss 的定义。黎曼度量代替 L2 Loss。
• Riemannian Flow Matching loss:
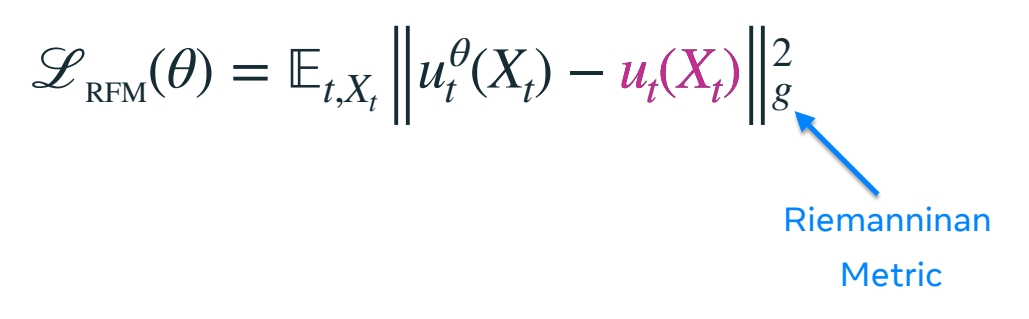
P102
• Riemannian Conditional Flow Matching loss:
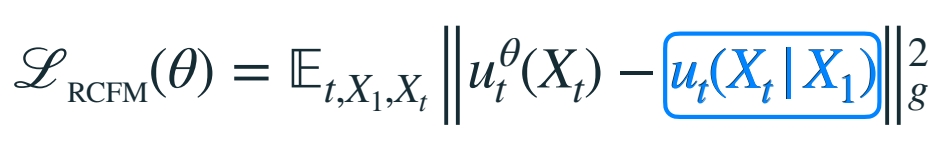
Losses are equivalent 的结论在这里同样适用:
$$ ∇_θℒ_{RFM}(θ) = ∇_θℒ_{RCFM}(θ) $$
P103
Conditional Flows - Simple Geometries
flow matching 中的直线推广到这里就是测地线,因为测地线是流形上的最短路径。

For simple manifolds (e.g. Euclidean, sphere, torus, hyperbolic),测地线的计算具有闭式表达:
$$ \Psi _t(x_0|x_1)=\mathrm{exp} _{x_0}(\kappa (t)\mathrm{log} _{x_0}(x_1)),\quad t \in [0,1] $$
$$ \mathrm{Scheduler }\quad \kappa (t):\kappa (0)=0,\quad \kappa (1)=1 $$
这种情况,无需模拟就能计算条件流。
P104
Conditional Flows - General Geometries
对于一般的几何结构,可能存在两个问题:
-
Geodesics can be hard to compute
-
Concentrate probability at boundary
因此难以计算。
P105
Choose a premetric satisfying:
- Non-negative:\(d(x,y) ≥ 0\).
- Positive: \(d(x, y) = 0\) iff \(x = y\).
- Non-degenerate:\(∇d(x, y) ≠ 0\) iff \(x ≠ y\).
Build conditional flow satisfying:
$$ d(ψ_t(x_0|x_1),x_1) = \tilde{κ}(t)d(x_0,x_1) $$
$$ \mathrm{Scheduler} \quad \tilde{κ} (t) = 1 − κ(t) $$
为了解决以上问题,提出了一种新的度量方法。
P106
对时间求导,得到微分方程。
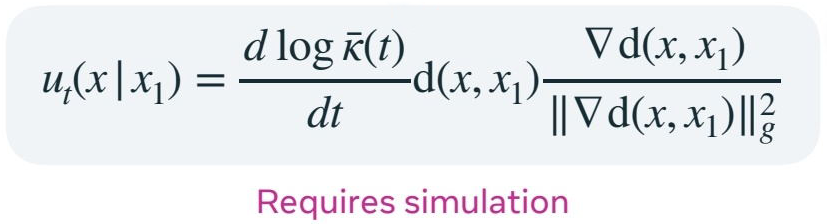
🔎 "Flow Matching on General Geometries" Chen & Lipman (2023)
P107
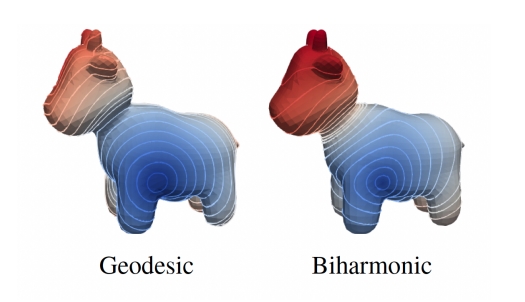
新度量方法与测地距离比较。
P108
Riemannian Flow vs. Score Matching

flow matching 的优势
(1)simulate free,速度快。PPT例子中快20倍。
(2)解 ODE 比解 SDE 容易
(3)\(u_t(X_t|X_1)\)是精确值,\(\nabla \mathrm{log}\) \(p_t(x|x_0)\) 是近似值。
P109
🔎 "Riemannian Score-Based Generative Modelling" De Bortoli et al. (2022)
🔎 "Flow Matching on General Geometries" Chen & Lipman (2023)
P110
相关工作
Equivariant Flow Matching:
🔎 "Fast Point Cloud Generation with Straight Flows" Wu et al. (2022)
🔎 "Equivariant flow matching" Klein et al. (2023)
🔎 "Equivariant Flow Matching with Hybrid Probability Transport" Song et al. (2023)
🔎 "Mosaic-SDF for 3D Generative Models" Yariv et al. (2023)
Riemannian Flow Matching:
🔎 "Flow Matching on General Geometries" Chen & Lipman (2023)
🔎 "SE(3)-Stochastic Flow Matching for Protein Backbone Generation" Bose et al. (2023)
🔎 "Sequence-Augmented SE(3)-Flow Matching For Conditional Protein Backbone Generation" Huguet et al. (2024)
🔎 "FlowMM: Generating Materials with Riemannian Flow Matching" Miller et al. (2024)
🔎 "FlowLLM: Flow Matching for Material Generation with Large Language Models as Base Distributions" Sriram et al. (2024)
🔎 "Metric Flow Matching for Smooth Interpolations on the Data Manifold" Kapuśniak et al. (2024)
本文出自CaterpillarStudyGroup,转载请注明出处。
https://caterpillarstudygroup.github.io/ImportantArticles/