Flow Matching Basics

P6
WHAT IS FLOW MATCHING?
A scalable method to train flow generative models.

HOW DOES IT WORK?
Train by regressing a velocity, sample by following the velocity

P11

增量生成方法

Marginal probability path

flow matching属于增量生成方法，需要学习边缘概率路径。
边缘概率路径是指，任意一个特定的 $t$ 时刻，$X_t$ 所属于的分布 $p_t$。即连续时间上的分布簇。

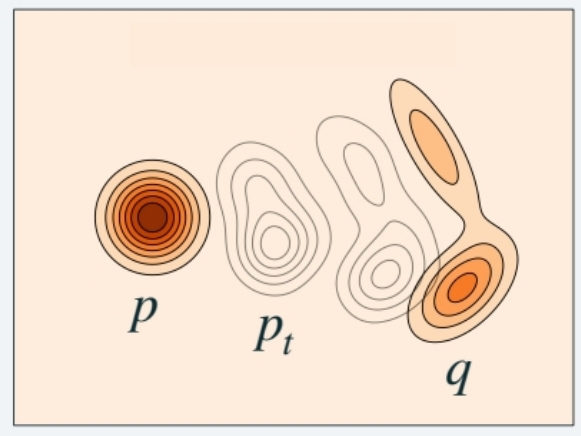
生成模型最重要的是，边缘概率路径以 $P$ 分布开始，以 $Q$ 分布结束。

P12

三种增量生成模型的特点

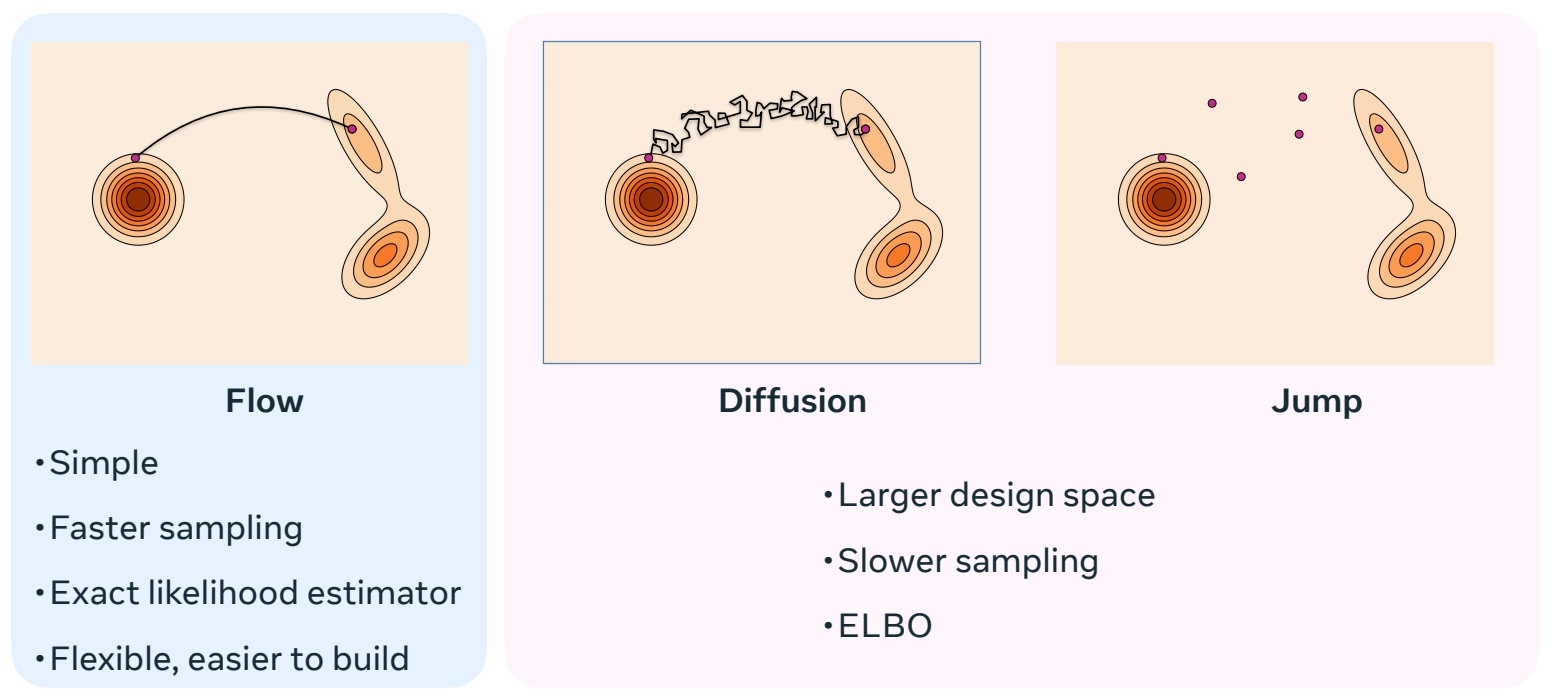
相比于其它增量生成方法，流的特点：(1) 确定性，已知 $X_t$，那么 $X_{t+h}$ 是确定的。(2) 平滑
流的优势：(1) sample 速度快 (2) 可以构建模型似然的无偏估计器。
Diffusion 和 Jump 具有更大的设计空间，因此具有更多生成能力。

P13

Flow 生成模型

Flow 的参数化

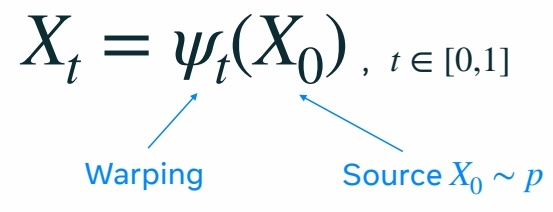
$\Psi_t$ 是 flow 生成模型的转移函数。
$\Psi_t$ 是一个双射函数，因此它可以重塑空间而不丢失信息。
通过对高维空间的 warping，使 $P$ 分布逐步变为 $Q$ 分布。
双射函数的特性：

一一对应：每个输入对应唯一的输出，且每个输出都被某个输入映射到。
可逆性：存在逆函数 $ f^{-1}: Y \to X $，满足 $ f^{-1}(f(x)) = x $ 且 $ f(f^{-1}(y)) = y $。

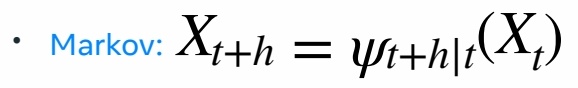
flow Model 是一个马尔可夫过程。
马尔可夫过程（Markov Process）是一类具有无记忆性（马尔可夫性质）的随机过程，其核心特点是未来状态仅依赖于当前状态，而与历史状态无关。

直接参数化会遇到的问题

对两个双射函数做线性组合，得到的函数不能保持其双射的特性，因此，基于双射函数的模型难以被参数化。

$$ \alpha X_ {t|1}+\beta X_ {t|2}\ne \Psi _ t(\alpha X_ {t|1}+\beta X_ {t|2}) $$

网络模型中通常包含大量线性组合，激活函数等会破坏双射性的结构，因此很难让网络学到一个双射函数。
“模型的参数化”（Parameterization of a Model）是指用一组可调整的参数（Parameters）来定义模型的结构和功能的过程。它是模型设计的核心步骤，决定了模型如何从输入数据中学习规律、进行预测或生成输出。包括（设计模型结构、连接方式，定义参数如何初始化，哪些参数可以被优化）。

P14

利用速度对流做参数化

因此利用速度对流做参数化。在这里，速度是指 $P_t$ 分布中的每个 sample 向 $Q$ 分布中对应 sample 变化的速度（快慢和方向）。
Flow 和 velocity 是可以互相转化的。对 Flow 做微分可以得到 velocity，对 velocily 解常微分方程，可以得到 Flow.

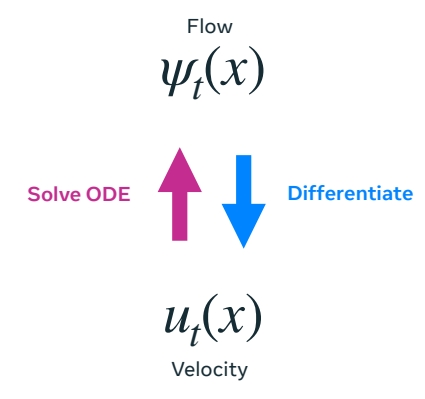
使用速度的好处：速度是线性的，可以相加或分解，因此可以对速度做参数化。
使用速度的缺点：需要对 sample 出速度做 ODE，解出图像。

$$ \frac{d}{dt} \Psi _t(x)=u_t(\Psi _t(x)) $$

$$ \frac{d}{dt}\Psi _t(\alpha X_1+\beta X_2)=\alpha u_t(\psi _t(X_1))+\beta u_t(\psi _t(X_2)) $$

P15

Velocity $u_t$ generates $p_t$ if

$$ X _t=\Psi _t(X_0)\sim p_t $$

使用速度来定义边缘概率路径，$\Psi_t$ 是基于速度的转移函数。

P16

Flow Matching 的训练

学习一个速度模型，由速度得到边缘路径概率 $P_t$，使得 $P_0 = P$， $P_1= Q$

P17

Sampling a flow model

Flow Matching 的推断：
(1) 从 $P$ 分布中 sample 一个 noise
(2) 根随速度（解ODE）得到对应在 $Q$ 分布中的 sample。

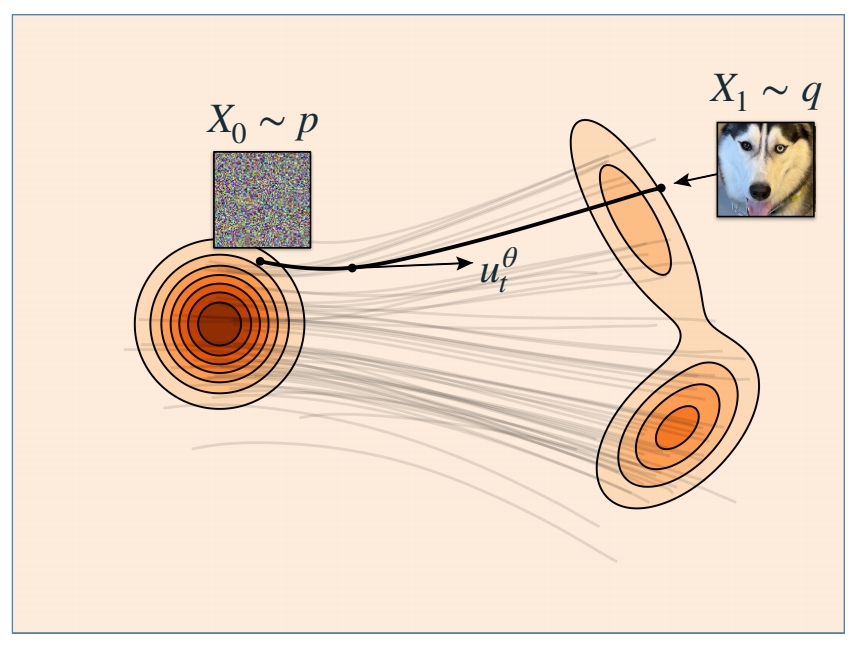
$$ \frac{d}{dt} X_t=u^0_t(X_t) $$

Use any ODE numerical solver.
One that works well: Midpoint

P19

Simplest version of Flow Matching

flow matching 的训练

(1) 随机构造源 $X_0$ 和目标 $X_1$。
(2) 在 [0，1] 区间随机采样一个时间步 $t$。
(3) $X_t$ 是 $X_0$ 与 $X_1$ 的线性组合。
(4) $X_t$ 是网络输入，让网络输出逼近$X_1-X_0$。

$$ \mathbb{E } _{t,X_0,X_1}||u_t^0(X_t)-(X_1-X_0)||^2 $$

🔎 "Flow Matching for Generative Modeling" Lipman el al. (2022)
🔎 "Flow Straight and Fast: Learning to Generate and Transfer Data with Rectified Flow" Liu et al. (2022)
🔎 "Building Normalizing Flows with Stochastic Interpolants" Albergo et al. (2022)

P20

这里没有对 $X_0$ 和 $X_1$ 所属的分布作限制。 $X_0$ 和 $X_1$ 可以是独立的噪声和图像，也可以是具有某种关系（例如黑白与彩色）的 pair data。

Why does it work?

• Build flow from conditional flows

如何从一个更简单的速度或流（称为条件流）构建一个速度或流。条件流是指一些简单的，固定的部分。

• Regress conditional flows

通过观察更简单的条件流来学习复杂的部分。

P21

局部问题

假设目标分布只有 $X_1$ 这一个点，那么流和速度是这样的。

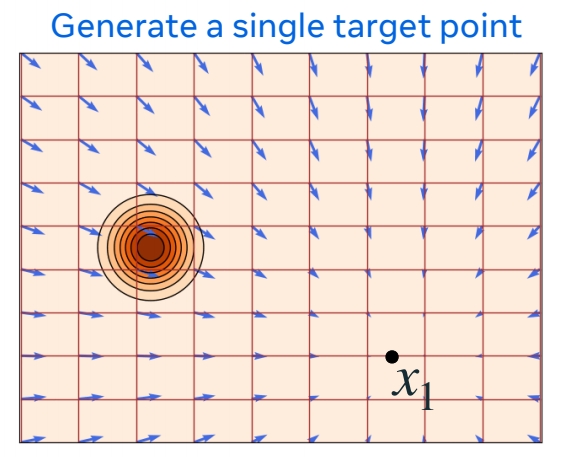
$$ X_t=\Psi _t(X_0|x_1)=(1-t)X_0+tx_1 $$

这是一个条件流。
$p_{t|1}(x|x_1)$ 是 conditional probability
$u_t(x|x_1)$ 是 conditional velocity，是常数。

P22

全局问题

实际的 $Q$ 分布包含很多 $x_1$ 这样的 sample，每一个 sample 都可以作为一个 condition，得到一个 $P_{t|条件}$ ，综合所有 $P_{t|条件}$ 得到的 $p_t(X)$ 是这 $P_{t|条件}$ 的期望。可以证明，$p_t(X)$ 以 $P$ 开始，以 $Q$ 结束。对 $Q$ 分布中的所有的 $x_1$，对 $U_t(X|X_1)$ 取平均，得到生成“边缘概率路径”的速度。
$p_t(x)= \mathbb{E} _ {X_ 1}p_{t|1}(x|X_ 1)$
$u_t(X)$ 也可以以这种方式得出。

$u_t(x)=\mathbb{E} [u_t(X_t|X_1)|X_t=x]$

这个速度场称为边缘速度。

P23

Theorem*: The marginal velocity (边缘速度) generates the marginal probability path (边缘概率路径)。

以上公式中的期望，实际含义是“平均”。

P24

conditional loss

目标函数：回归边缘速度场。

(1) 直接回归边缘速度场

$$ ℒ_{FM}(θ) = \mathbb{E} _{t,X_t}||u^θ_t (X_t) − u_t(X_t)||^ 2 $$

其中，$u_t(X_t)$ 是通过许多数据计算出的均值(根据上文中的公式)。
(2) 回归条件速度

$$ ℒ_{CFM}(θ) = \mathbb{E} _{t,X_1,X_t}||u^θ_t (X_t) − u_t(X_t|X_1)||^ 2 $$

Theorem: Losses are equivalent,

$$ \nabla_θℒ_{FM}(θ) = \nabla_θℒ_{CFM}(θ) $$

结论：仅回归条件速度，与直接回归速度相同。
使用条件分布(公式 2)相比于公式 1 的好处是，可以逐个样本去计算，而不需要对整个数集做平均。

P25
Theorem: Losses are equivalent if $D$ is a Bregman divergence.

更进一步，使用任意的 Bregman Divergence Loss $(D(\cdot ,\cdot ))$ 散度代替 $L2(||\cdot ,\cdot ||^2)$，都能得到相同结论，L2 Loss 只是其中一种。

P26

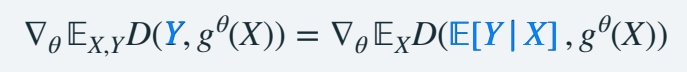
因为要学习的是一个“期望”。

P27

How to choose $ψ_t(x|x_1)$?

Optimal Transport minimizes Kinetic Energy

在上文中，定义

$$ ψ _t(x|x_1)=tx_1+(1-t)x $$

这样定义，是基于“最小化动能”的考虑。

如果最小化动能，能让路径变得直，且速度恒定。
所以将 $ψ _t(X_0|X_1)$ 定义为 $X_0$ 和 $X_1$ 连线上的一个点，其中 $X_0$ 可以是空间中任意一点定义为 $X$ 。

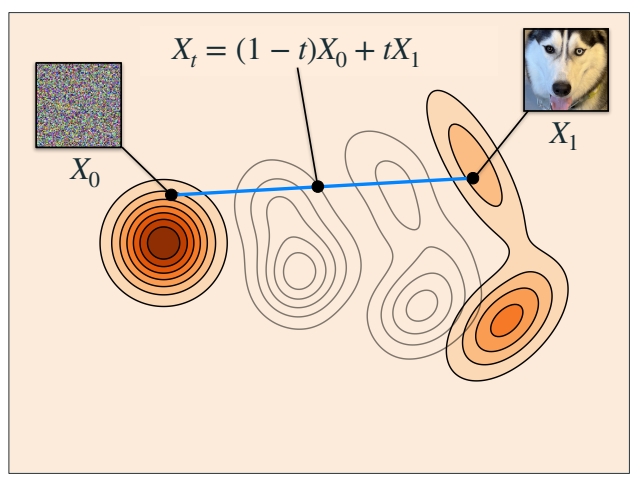
直接优化动能不容易，因为它不依赖于具体的条件。因此给它设定一个 Jensen bound，来限制边缘速度的动能。

Jensen bound 是具体的条件 $(X_0,X_1)$ 下的期望。
当 $X_0$ 和 $X_1$ 确定时，Jensen bound 可以被算出来，也可以(通过优化$ψ _t$)被最小化。

结论： 当 $ψ _t(x|x_1)$ 定义为 $tX_1+(1-t)X$ 时，Jensen bound 被最小化，此时 $X_0$ 到 $X_1$ 是直线。

Linear conditional flow总结:
• Minimizes bound，而不是直接优化动能。
• Reduces Kinetic Energy of initial coupling
把 $ψ _t$ 代入 Jensen bound 公式可得出此结论。

• Exact Optimal Transport for single data points
如果 $Q$ 分布中只有一个 $X_1$。此时公式左右两边相等，是最优传输。

• Not Optimal Transport (but in high dim straighter)
如果 $Q$ 分布里不止一个点，不是最优传输，$X_0$ 到 $X_1$ 也不是直线。

🔎 "Flow Straight and Fast: Learning to Generate and Transfer Data with Rectified Flow" Liu et al. (2022)
🔎 "On Kinetic Optimal Probability Paths for Generative Models" Shaul et al. (2023)

P29
好的最优传输，可以通过单个欧拉步骤采样。

$$ \frac{d}{dt} \Psi _t(x)=u_t(\Psi _t(x)) $$

$$ ℒ_{CFM}(θ) = \mathbb{E}D(u^θ_t (X_t),u_t(X_t|X_1)) $$

D 是一个 Bregman 散度，L2 Loss 是其中一种，根据上文中 $ψ _t$ 的定义，把L2 和条件速度代入公式得：对于特定的 $X_0$ 和 $X_1$ ， $X_1-X_0$ 是条件路径的条件速度。

$$ ℒ_{CFM}(θ) = \mathbb{E}||u^θ_t (X_t)-(X_1-X_0)||^ 2 $$

因此，这个算法是特定条件流 + 特定 Loss 下的一个 flow matching 实例。

P30

Affine paths

在前面的方法中，$ψ_t(x|x_1)$ 是 $x$ 与 $x_1$ 的线性组合，这只是一种选择。现在假设其为仿射组合。

这种情况下，$X_0$ 到 $X_1$ 不再是直线。
由此得到不同的参数化速度的方式，例如：
(1) $u_t(x)=\frac{d\psi t}{dt}$ ，直接预测速度

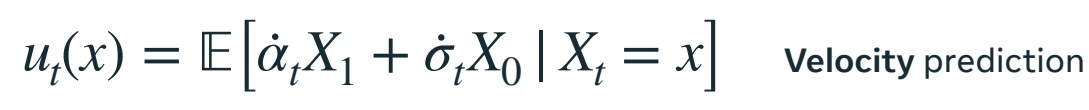
(2) 源预测：通过 $X_0$ 的条件期望来参数化速度。预测 $X_0$ ，再转化为 $x$ 的速度

(3) 目标预测类似，预测 $X_1$ ，再转化为 $x$的速度

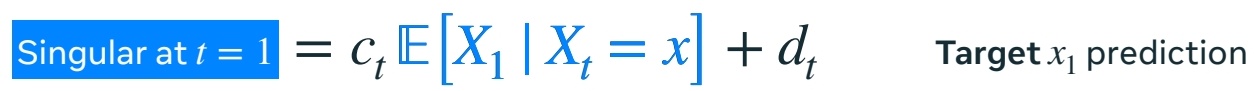
根据 $\alpha _t$ 和 $\sigma _t$ 的定义不同，推导出的 $a_t,b_t,c_t,d_t$ 不同。
以上公式中的“期望”部分，都是网络要预测的部分。预测的内容不同，最终目的都是为了求 $x$ 的速度。

P31

Gaussian paths

目前为止，没有对源分布 $P$ 和目标分布 $Q$ 做任何假设。
如果假设 $P$ 是一个高斯分布，$P$ 和 $Q$ 是独立的，这个过程即与 diffusion 的 ODE 过程吻合。

$$ p(x) = 𝒩(x |0 , I) \quad π_{0,1}(x_0, x_1) = p(x_0)q(x_1) $$

diffusion 的噪声预测，在 $x$ 接近噪声时(初始 steps)会有奇异性问题。

P32 　

Affine and Gaussian paths

参数比较

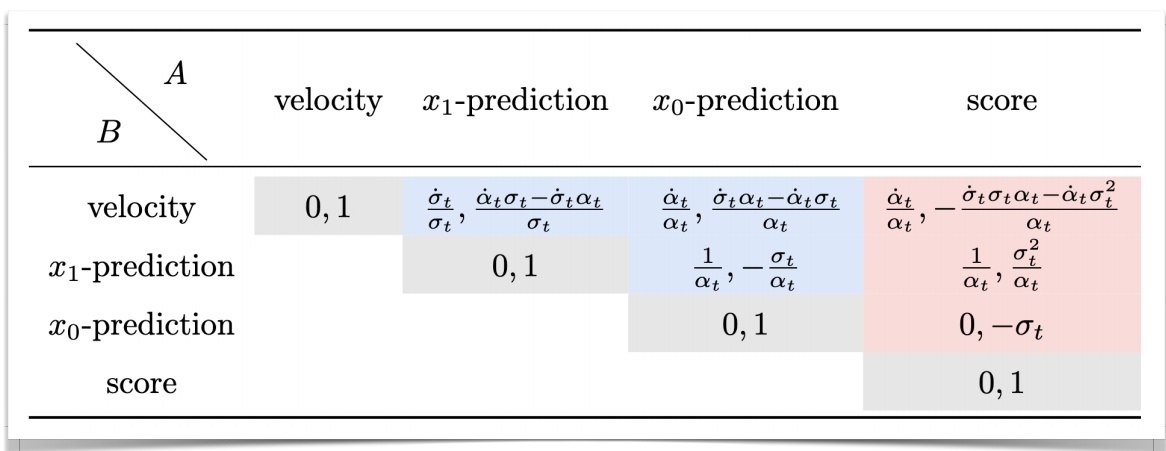
蓝色部分适用于所有的仿射路径(包括高斯 path)。粉色部分仅适用于高斯 path.
[❓] 表格怎么看？

P33

flow matching 与确定性 diffusion 之间的关系:
1.diffusion 通过定义 forward process 然后再反转来生成概率路径。
flow matching 通过将所有已知的条件概率路径的聚合来生成概率路径。
2.diffusion 构造了 forward prossess，需要一个根据 forward process 构造条件概率的闭式解，因此会要求 $P$ 是高斯，且 $P$ 和 $Q$ 独立。
flow matching 没有这样的限制，$P$ 和 $Q$ 可以是任意的分布。

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/ImportantArticles/