P111

Model Adaptation

P112

You’ve trained a model. What next?

已有一个预训练模，可以做什么？

P113

Faster Sampling

P114

Recitde Flow-Faster sampling by straightening the flow

方法

$$ ℒ(θ) = \mathbb{E} _ {t,(X_0,X_1)∼π_ {0,1}^0}||u^θ_t (X_t) − (X_1 − X_0)||^2 $$

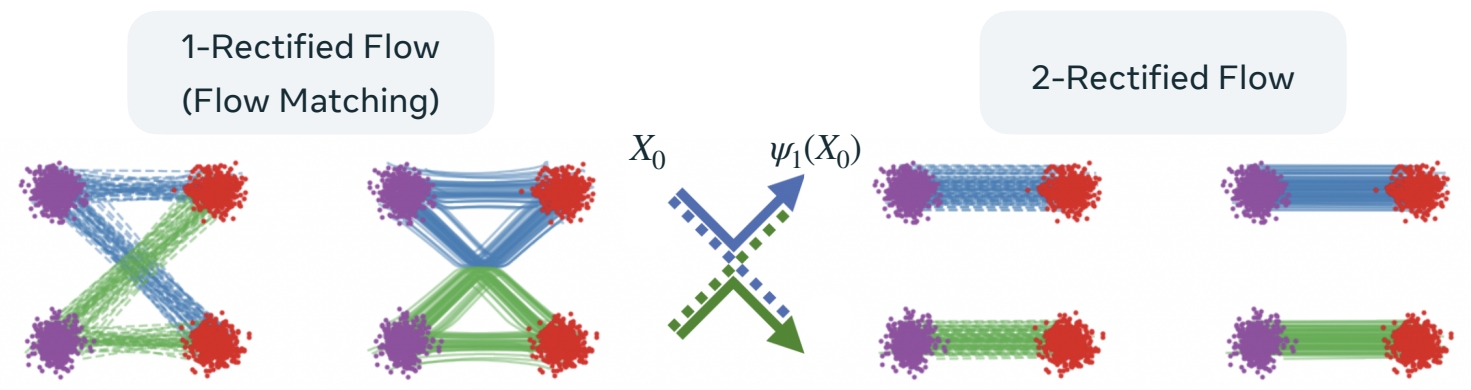
Rectified Flow refits using the pre-trained (noise, data) coupling.
Leads to straight flows.

Rectified Flow：让 flow 从源直接到目标。
第1步：训练 flow matching，flow matching 模型定义了源和目标的耦合关系，也得到了噪声与数据的 pair data.
第2步：用 pair data 继续训练。

🔎 “Flow Straight and Fast: Learning to Generate and Transfer Data with Rectified Flow” Liu et al. (2022)

P115

P116

局限性

Enforcing straightness restricts the model. Often a slight drop in sample quality

🔎 “InstaFlow: One Step is Enough for High-Quality Diffusion-Based Text-to-Image Generation” Liu et al. (2022)

P118

Faster sampling by self-consistency loss

增大 $h$，在 $x_t$ 和 $X_{t＋h}$ 之间建立 shortcut，类似于 diffusion 中的蒸馏方法。

局限性

Shortcuts with $h$ >0 do not work with classifier-free guidance (CFG).
CFG weight can & must be specified before training.

short cuts 直接预测流而不是速度，流是非线性的，不能对结果加权组合，因此不能结合 CFG.
针对此问题的 workaround：预置 CFG 权重

🔎 “One Step Diffusion via Shortcut Models” Frans et al. (2024)

P124

Faster sampling by only modifying the solver

以上两种方法，都需训练。此方法不需要训练，而是修改 solver.

补充：关于调度器．$\beta, \alpha _t$ 和 $\sigma _t$的 trick．

Can adapt pre-trainedmodels to different schedulers.

有一个用 scheduler A 训练好的模型，现在要一个用 scheduler B 继续训练，这两个模型是什么关系？

结论：这两个 scheduler 及其 flow 可以通过 $X$ 的缩放和时间的重参数化关联起来。
时间重参数化是指，匹配两个 scheduler 的 SNR 和 scaling。

Related by a scaling & time transformation:

如图所示，调整 scheduler,流会表现出不同，但 $X_0$ 与 $X_1$ 的耦合关系不变。

🔎 “Elucidating the design space of diffusion-based generative models” Karras et al. (2023)

P126

修改 scheduler 的例子

Bespoke solvers:
Decouples model & solver.
Model is left unchanged.
Parameterize solver and optimize.

模型与 solver 解耦：模型不变，仅优化求 solver.
向 solver 中传入参数(表达 scheduler)，优化这些参数相当于在优化 scheduler。

Can be interpreted as finding best scheduler + more.

Solver consistency: sample quality is retained as NFE → ∞.

由于仅优化solver，好处：
1．可以利用 solver 的一致性，把步数取到无穷大，仍然能准确地解 ODE。做法是，用数据集 A 训练生成模型后，用数据集 B 训练 scheduler 的新参数。
2．在不同的模型(不同数据集、分辨率等训练出来的模型)之间可迁移。

Bespoke solvers can transfer across different data sets and resolutions.

局限性：

虽然能(不重训生成模型)直接迁移到另一个模型，但比在另一个模型上蒸馏(重训)效果要差一点。

P127

However, does not reach distillation performance at extremely low NFEs.

P128

Inverse Problems (Training-Free)

Inverse Problem：填充、去糊、超分、编辑。
与上节中的 data coupling 中要解决的问题不同的是，这里要利用在完全干净的数据集上训好的预训练模型，不经过重训，得到解决 Inverse Problem 的效果。

P133

Solving inverse problems by posterior inference

$x_1$ 为干净图像，$y$ 为噪声图像。

用高斯来近似其中未知的部分 (score function)
score function 可能是 multi 的，但实验证明仅用高斯也能有比较好的效果。

P134

局限性

Typically requires known linear corruption and Gaussian prob path.
Can randomly fail due to the heuristic sampling.

🔎 “Pseudoinverse-Guided Diffusion Models for Inverse Problems” Song et al. (2023)
🔎 “Training-free Linear Image Inverses via Flows” Pokle et al. (2024)

P135

Solving inverse problems by optimizing the source

观察结论

Don’t want to rely on likelihoods / densities.

预训练一个生成模型，然后有这个模型来评估数据，评估结果很不可靠，它把数据集中的数据评估为低密度，非数据集中的数据评估为低密度。
因为，高密度$\ne$ 高采样率。

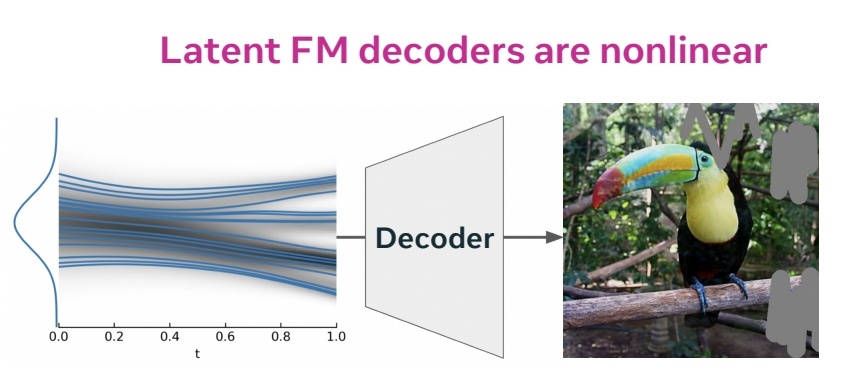
Have observation $y$ being nonlinear in $x_1$.

$y$ 是真实图像，$X_1$ 是模型 sample,$X_1$ 与 $y$ 之间差了一个 Decoder.因此它们的关系是非线性的。

🔎 “Do Deep Generative Models Know What They Don't Know?” Nalisnick et al. (2018)

P138

方法

逆问题转化为优化问题。

$$ X_1=\psi (X_0) $$

$\psi $ 是预训练的生成模型，不优化 $\psi $ 的参数，那就优化$X_0$ 。因为 $\psi $ 是一个平滑、可逆、可微的函数。

P139

特点与局限性

$$ \min_{x_0} L(\psi ^\theta _1(x_0)) $$

Theory: Jacobian of the flow $\nabla _{x_0}\psi ^\theta_1$ projects the gradient along the data manifold.

Intuition: Diffeomorphism enables mode hopping!

P140

Simplicity allows application in multiple domains.

Caveat: Requires multiple simulations and differentiation of $\psi ^\theta _1$.

求导链路很长，计算成本很高。

🔎 “D-Flow: Differentiating through Flows for Controlled Generation” Ben-Hamu et al. (2024)

P141

Inverse problems references

Online sampling methods inspired by posterior inference:

🔎 “Diffusion Posterior Sampling for General Noisy Inverse Problems” Chung et al. (2022)
🔎 “A Variational Perspective on Solving Inverse Problems with Diffusion Models” Mardani et al. (2023)
🔎 “Pseudoinverse-Guided Diffusion Models for Inverse Problems” Song et al. (2023)
🔎 “Training-free Linear Image Inverses via Flows” Pokle et al. (2023)
🔎 “Practical and Asymptotically Exact Conditional Sampling in Diffusion Models” Wu et al. (2023)
🔎 “Monte Carlo guided Diffusion for Bayesian linear inverse problems” Cardoso et al. (2023)

Source point optimization:

🔎 “Differentiable Gaussianization Layers for Inverse Problems Regularized by Deep Generative Models" Li (2021)
🔎 “End-to-End Diffusion Latent Optimization Improves Classifier Guidance” Wallace et al. (2023)
🔎 “D-Flow: Differentiating through Flows for Controlled Generation” Ben-Hamu et al. (2024)

方法 1：通过修改 sample 方法来逐步接近目标。这些方法大多数受到某种后验推断的启发，可以在准确性和效率之间 trade off.
方法 2：简单但开销很大。

P144

Reward Fine-tuning

Data-driven and reward-driven fine-tuning



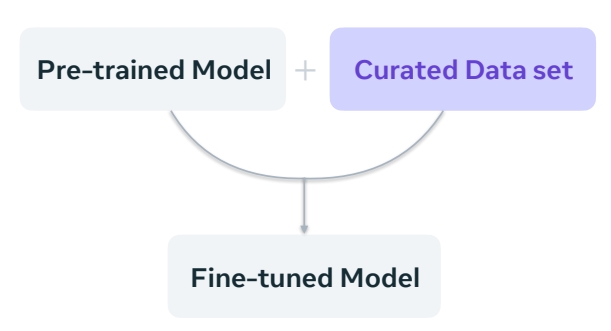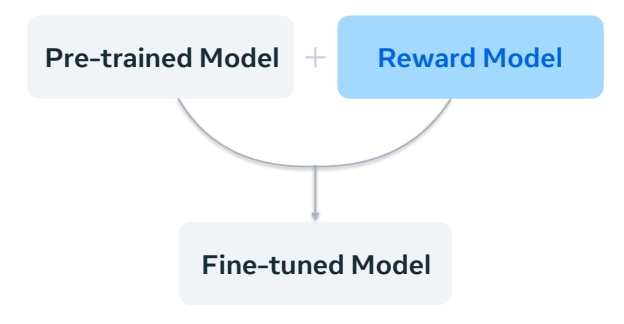A lot of focus put into data set curation through human filtering.	Can use human preference models or text-to-image alignment.

Data-driven 的关键在于精心准备数据集。
Reward-driven 不增加训练数据，而是给模型输出一个 reward。finetune 的目标是生成得分高的 sample.
此处仅介绍后者。

P145

Reward fine-tuning by gradient descent

Initializing with a pre-trained flow model $p^\theta$：

$$ \max_{\theta } \mathbb{E} _{X_1\sim p^\theta }[r(X_1)] $$

Optimize the reward model with RL [Black et al. 2023]
or direct gradients [Xu et al. 2023, Clark et al. 2024]

P146
优点：
不同的奖励模型可以组合，得到综合的效果。

局限性：
Requires using LoRA to heuristically stay close to the original model.
Still relatively easy to over-optimize reward models; “reward hacking”.

这种方法没有 GT，所以生成结果有可能对 reward model 过拟合。因此需要使用 LoRA.

🔎 “Training diffusion models with reinforcement learning” Black et al. (2023)
🔎 “Imagereward: Learning and evaluating human preferences for text-to-image generation.” Xu et al. (2023)
🔎 “Directly fine-tuning diffusion models on differentiable rewards.” Clark et al. (2024)

P149

Reward fine-tuning by stochastic optimal control

方法1：RLHF

和直接优化相比，RLHF 将一个预训练分布倾科为能得到更高奖励的分布。

正则化：微调模型分布应与预训练模型分布接近。常用方法是增加KL 项，如下面公式蓝色部分。但这里不这样用。因为，我们要优化的不是概率路径，而是与 $X_0$ 相关的 something.
这里采用公式（3），即引入 value function bias．
value function bias 是 $X＝X_0$时，所有可能的 $X_1$ 的期望。

P150
原理：

Intuition: Both initial noise $p(X_0)$ and the model $u_t^{base}$ affect $p^{base}(X_1)$.

原理：某一时刻的分布受到 noise 分布和模型的共同影响，即使是同一个预预训练模型改变 noise 的分布，那么 $X_1$ 的分布也会改变。
由于 $X_1$ 同时受模型和 noise 分布的影响，那么 RLHF 同时优化这两个因素。

[Uehara et al. 2024] (即 RLHF) proposes to learn the optimal source distribution $p^\ast (X_0)$.

方法2：Adjoint Matching

或者，改变采样方法，让 $X_0$ 分布与 $X_1$ 分布独立。那么此时，value function 是一个常数。

[Domingo-Enrich et al. 2024] proposes to remove the dependency between $X_0, X_1$.

$$ p^\ast (X_{(0,1)})=p^{base}(X_{(0,1)})\mathrm{exp} (r(X_1)+const.)\Rightarrow p^\ast (X_1)\propto p^{base}(X_1)\mathrm{exp} (r(X_1)) $$

🔎 “Fine-tuning of continuous-time diffusion models as entropy regularized control” Uehara et al. (2024)

P151

🔎 “Adjoint matching: Fine-tuning flow and diffusion generative models with memoryless stochastic optimal control” Domingo-Enrich et al. (2024)

这篇论文的主要内容：
1．使用 flow matching 在真实图像上训练后，再使用 ODE 采样，能得到真实的输出。
2．把 ODE 过程改成无记忆 SDE（强制 $X_0$ 与 $X_1$ 独立），那么在早期的 sample step 实际上没有什么收益，因为那时候 $X$ 大部分都是噪声。因此 SD 的采样结果不符合预训练的分布。
3．把 2 用于 finetune 的过程，因此 finetune 过程，不使用 flow 的 sample 方式，而是 SDE 的 sample 方式。
4．finetune 之后，可以把 SDE 换回成 ODE。

P152

Reward fine-tuning 总结

Gradient-based optimization:

🔎 “DPOK: Reinforcement Learning for Fine-tuning Text-to-Image Diffusion Models” Fan et al. (2023)
🔎 “Training diffusion models with reinforcement learning” Black et al. (2023)
🔎 “Imagereward: Learning and evaluating human preferences for text-to-image generation.” Xu et al. (2023)
🔎 “Directly fine-tuning diffusion models on differentiable rewards.” Clark et al. (2024)

Stochastic optimal control:

🔎 “Fine-tuning of continuous-time diffusion models as entropy regularized control” Uehara et al. (2024)
🔎 “Adjoint matching: Fine-tuning flow and diffusion generative models with memoryless stochastic optimal control” Domingo-Enrich et al. (2024)

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/ImportantArticles/

ImportantArticles