P2

Outline

🔎 SIGGRAPH 经典的蒙皮课程。
Many images are from: https://skinning.org/
Alec Jacobson, Zhigang Deng, Ladislav Kavan, and J. P. Lewis. 2014.
Skinning: real-time shape deformation.
In ACM SIGGRAPH 2014 Courses (SIGGRAPH '14)

P7

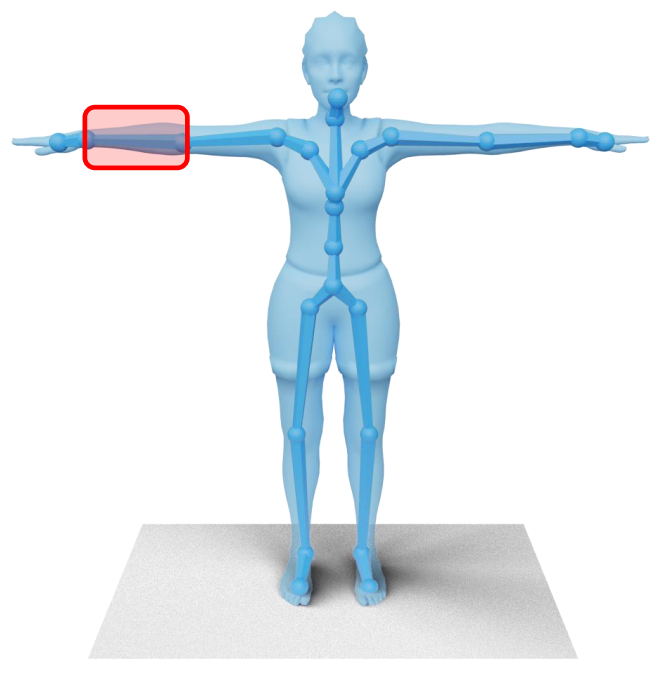
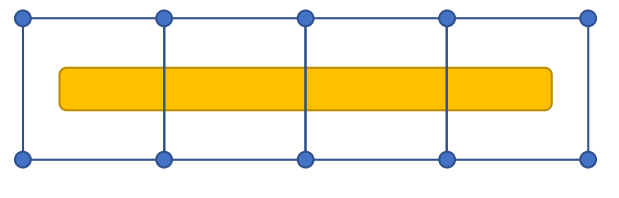
Skinning Deformation

绑定与蒙皮概念

✅ Rigging：创建脸部控制器或身体骨骼。黄色为在 Mesh 顶点内放置的骨骼。
✅ Sinning：让控制器带动皮肤运动。或让 Mesh 顶点跟着骨骼运动。

骨骼代理的角色驱动的局限性

1. 非刚性形变:
   • LBS（线性混合蒙皮）无法表达肌肉膨胀、软组织形变
   • 解决方案：PartMM（Part-aware Mixture Model）替代LBS
2. 高频细节丢失:
   • 骨骼代理只能捕获低频运动（关节旋转）
   • 解决方案：法线修正、位移残差学习

P12

Skinning Deformation

计算方式一

✅ 骨骼运动的旋转和平移分别为 \(R\) 和 \(t\)，关节的位置和朝向则变成了 \({Q}'\) 和 \({o}'\).
✅ 求 \(x\) 的新位置 \({x}'\). 本质上就是坐标系变换：世界坐标系 → \({o}\) 坐标系 → \({o}'\) 坐标系 → 世界坐标系

P13

计算方式二

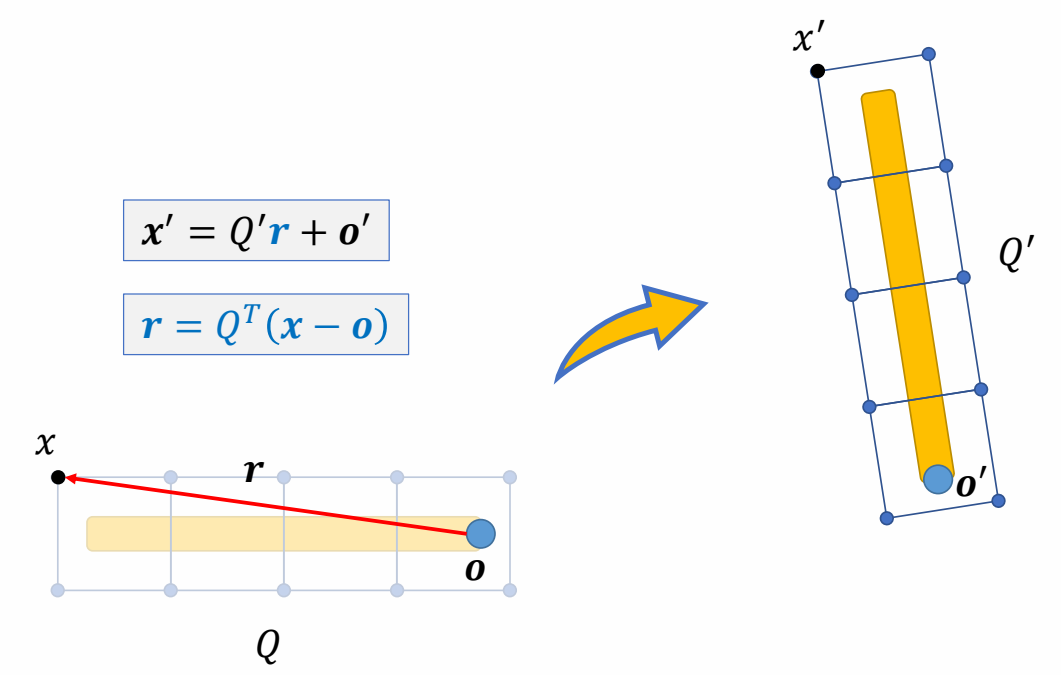
✅ \(r\) 为 \(x\) 在骨骼坐标的表达，用 \(r\) 计算更简洁。

P16

Bind Pose

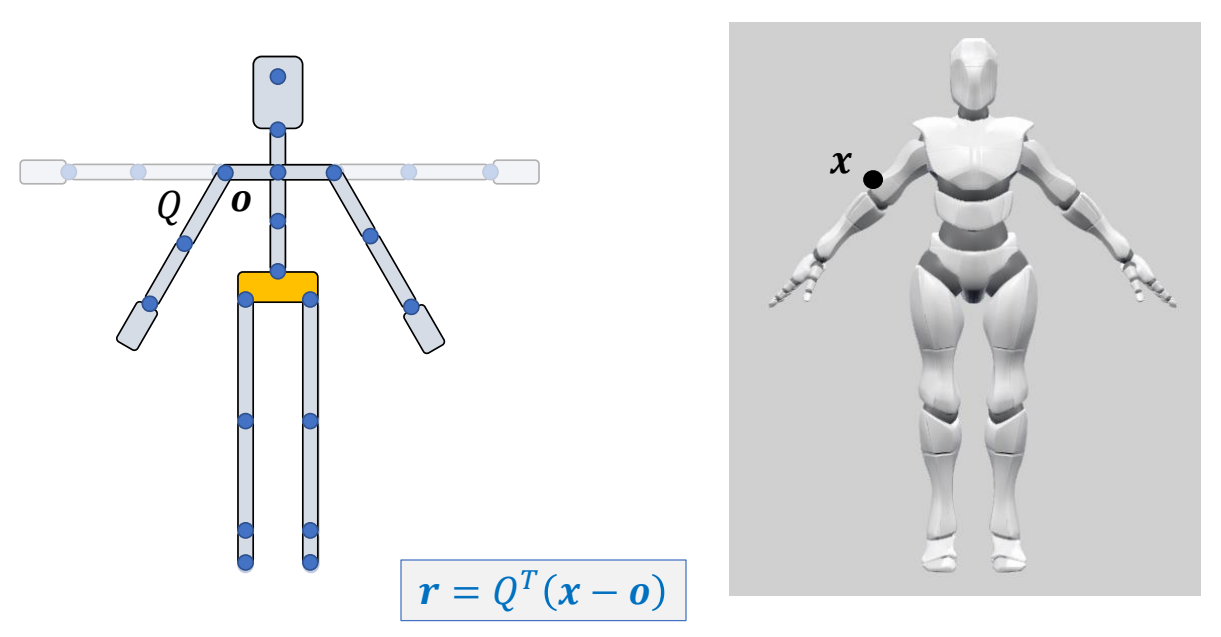
✅ 当骨骼参考姿态与 Mesh 参考姿态不一致时，需要先旋转骨骼到 Mesh 姿态。

P20

Skinning Deformation - 2 joints

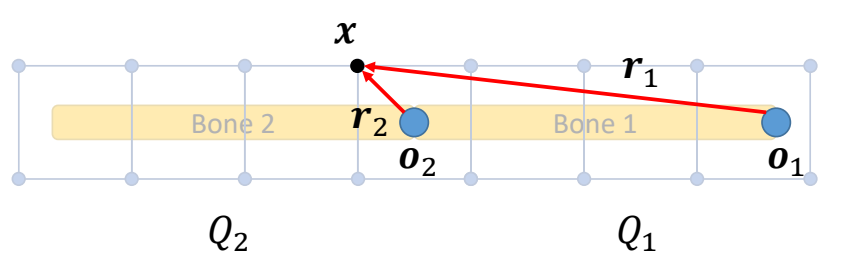
$$ r_2=Q^T_2(x-o_2) \quad \quad r_1=Q^T_1(x-o_1) $$

✅ 多骨骼场景，\(x\) 在关节 \(O_1\) 和 \(O_2\) 下分别 \(r_1\) 和 \(r_2\) 两种表达。

P23

✅ 得到的旋转后表达分别为 \({x}'_1\) 和 \({x}'_2\)，通过权重对它们结合。

P29

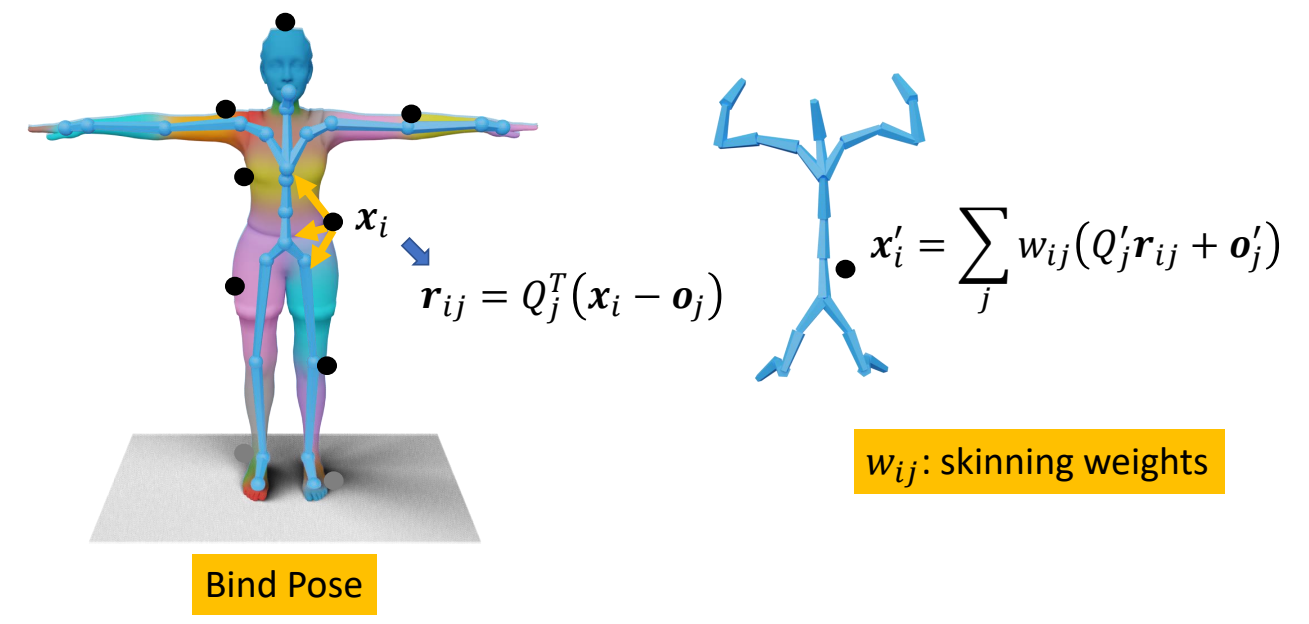
✅ 同时考虑所有 Mesh 顶点和所有关节。

补充：LBS 基础（

LBS 是最流行的角色蒙皮方法。它的核心公式：

$$ \mathbf{v} _{i} ^{t} = \sum _{j=1}^{|B|} w _{ij} \left( \mathbf{R} _{j} ^{t} \mathbf{p} _{i} + \mathbf{T} _{j} ^{t} \right) $$

通俗理解：

想象你有一块橡皮泥（顶点），它被钉在几根棍子（骨头）上。
每根棍子上都有一个钉子，钉子对橡皮泥的拉力就是权重 w。

当棍子移动时，橡皮泥的位置 = 每根棍子拉力 × 棍子移动距离 的总和

LBS 权重的约束条件

为了让 LBS 模型有意义，权重 \(w _{ij}\) 需要满足三个条件：

1. 非负性（Non-negativity）：\(w _{ij} \geq 0\)

   • 骨头不能"推"顶点，只能"拉"

2. 凸性/仿射性（Affinity）：\(\sum _{j=1}^{|B|} w _{ij} = 1\)

   • 所有骨头对一个顶点的总影响权重等于 1
   • 这保证了如果所有骨头都不动，顶点也不动

3. 稀疏性（Sparseness）：\(|\{w _{ij} | w _{ij} \neq 0\}| \leq |K|\)

   • 每个顶点最多被 \(|K|\) 根骨头影响
   • 在实际应用中，通常 \(|K| = 4\)（称为 4-bone skinning）
   • 这是为了 GPU 加速——每个顶点只需计算 4 个变换

刚性骨骼约束

旋转矩阵 \(\mathbf{R} _{j} ^{t}\) 必须满足正交约束：

$$ \mathbf{R} _{j} ^{t} {}^{T} \mathbf{R} _{j} ^{t} = \mathbf{I}, \quad \det(\mathbf{R} _{j} ^{t}) = 1 $$

通俗理解：

"刚性"意味着骨头不能被拉伸、压缩或剪切。
旋转只会改变方向，不会改变长度。

对比：
- 刚性旋转：把一本书转个角度，书还是原来的形状
- 非刚性变换：把一本书拉长、压扁、撕扯——这些都不允许

P31

Linear Blend Skinning (LBS)

$$ {x}'_ i= \sum_ {j=1} ^ {m} w _ {ij}({Q}'_ jr_{ij}+{o}'_j) $$

• Used widely in industry
• Efficient and GPU-friendly
  • Games like it

✅ Bind Pose：让骨骼与 Mesh 对齐，为 Bind Pose．
✅ Bind Pose 情况下 Motion 不一定为零。

P33

Automatic Skinning?

Pinocchio [Baran et al., 2007]

P37

Linear Blend Skinning (LBS)

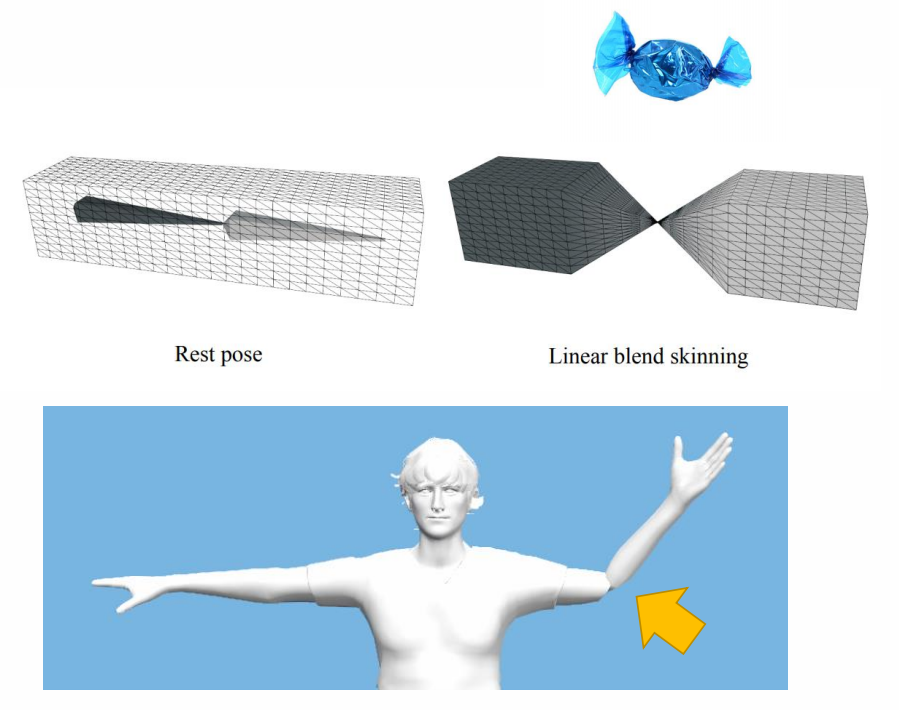
✅ 公式第一项对 \(R_j\) 所加权，所得到的很有可能不再是旋转矩阵。

存在的问题： Candy-Wrapper Artifact

P40

Advanced Skinning Methods

• Multi-linear Skinning (we will not cover this)

  • Multi-weight enveloping [Wang and Phillips 2002]
  • Animation Space [Merry et al. 2006]
  • ……

• Nonlinear Skinning

  • Dual-quaternion Skinning (DQS)
  • Skelebones (PartMM) — GaussiAnimate (ReadPapers/220): 用 Part-aware Mixture Model 替代 LBS。核心：(1) 用空间距离 softmax 计算 part affinity 概率替代人工皮肤权重；(2) 用 MLP 学习的非线性残差 \(x + \Delta T_j(x)\) 替代刚体变换，突破 LBS 线性上限，PSNR 比 LBS 高 17.3%。原本用于 3DGS 驱动，理论上也可用于 Mesh 驱动，但 Mesh 场景下面临三个问题：(1) MLP 推理比 LBS 矩阵乘法慢，不利于实时渲染；(2) MLP 输出可能跨帧跳跃，时间一致性不如 LBS 稳定；(3) 现有引擎全基于 LBS/DQS 构建，替换绑定方案工程成本高。Mesh 本身有拓扑约束兜底，LBS/DQS/SSD 已足够；PartMM 对没有拓扑的 3DGS 价值更大。

✅ DQ：对偶四元数。

P41

Non-linear Skinning

quaternions and SLERP

Can we use quaternions and SLERP?

P42

✅ 不行。原因：第一项与第二项必须要配合好，否则会乱掉。

P43

从公式角度来解释不行的原因

$$ {x}' _ i = ( \sum _ {j=1}^{m} w _ {ij} R _ j) x _ i+ \sum _ {j=1}^{m}w _ {ij}t_ j $$

$$ R \in SO(3) $$

$$ T_j=\begin{bmatrix} R_j & t_j\\ 0 &1 \end{bmatrix} \in SE(3) $$

✅ \(T_j\) 构成一个刚性变换群。

P46

Interpolation in 𝑆𝑂(3)

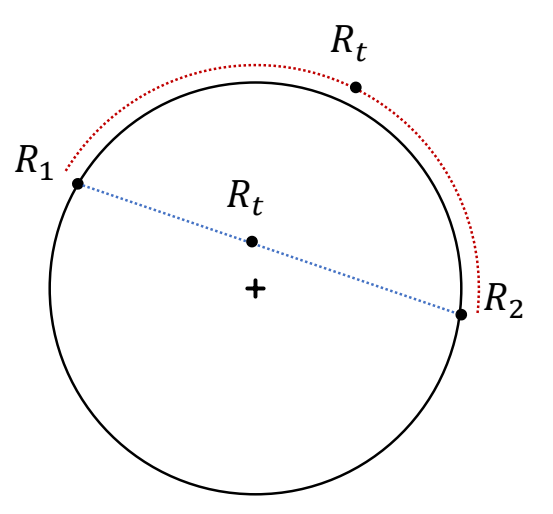
✅ 线性插值和 SLERP 插值 SO(3) 上。

P49

Interpolation in 𝑆𝐸(3)

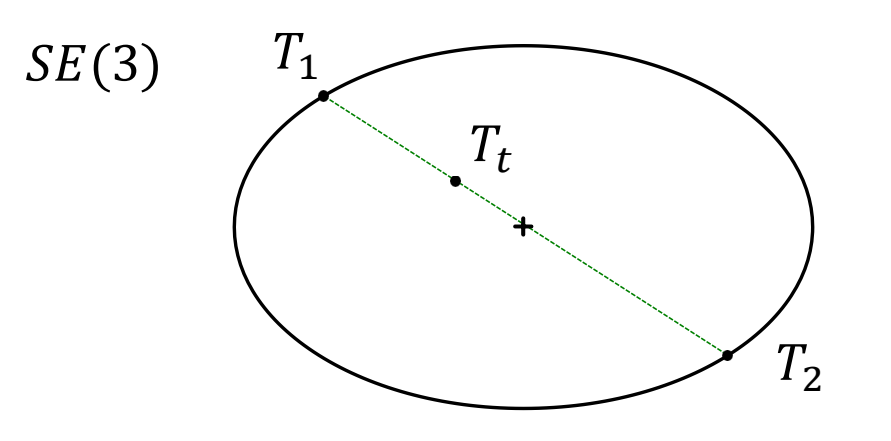
✅ SE（3）上的线性插值，插值到一个退化的点。

P51

Intrinsic Blending

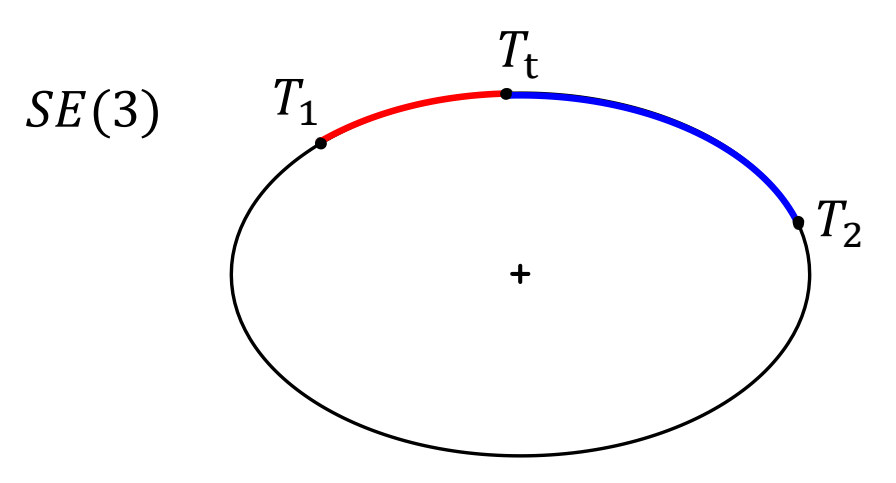
P52

Dual-Quaternion Skinning (DQS)

• Approximation of intrinsic averages in SE(3)

Ladislav Kavan, Steven Collins, Jiri Zara, Carol O‘Sullivan. Geometric Skinning with
Approximate Dual Quaternion Blending, ACM Transaction on Graphics, 27(4), 2008.

✅ 把旋转 ＋ 平移的刚性变换表达为对偶四元数。

P54

Dual Numbers

P55

Dual Quaternion

• Dual quaternion

$$ \hat{q} =q_0 + \varepsilon q_\varepsilon $$

$$ \text{where } \varepsilon^2=0 $$

A good note of dual-quaternion:
https://faculty.sites.iastate.edu/jia/files/inline-files/dual-quaternion.pdf

P56

Dual Quaternion

• Scalar Multiplication

$$ s\hat{q}=sq_r+sq_\varepsilon\varepsilon $$

• Addition

$$ \hat{q} _ 1 + \hat{q} _2=q _ {r1}+ q _ {r2} + \varepsilon (q _ {\varepsilon 1} + q _ {\varepsilon 2}) $$

• Multiplication

$$ \hat{q} _ 1 \hat{q} _ 2 = q _ {r1} q _ {r2} + \varepsilon (q _ {r1} q _ {\varepsilon 2} + q _ {r2} q _ {\varepsilon 1}) $$

P57

Dual Quaternion

• Dual quaternion

$$ \hat{q}=q_0+\varepsilon q_\varepsilon $$

• Conjugation

$$ \mathrm{I}:\hat{q}^* =q ^ * _ 0+\varepsilon q ^ * _ \varepsilon $$

$$ \mathrm{II}:\hat{q}^ {\circ} =q _ 0 - \varepsilon q _ \varepsilon $$

$$ \mathrm{III}: \hat{q} ^ \star = q ^ * _ 0 - \varepsilon q ^ *_ \varepsilon $$

$$ \quad \quad \quad \quad = ({\hat{q} ^ *}) ^ {\circ} = (\hat{q} ^ {\circ}) ^ * $$

$$ (\hat{q} _1\hat{q}_2)^\times =\hat{q} _1 ^\times \hat{q}_2^\times $$

• Norm

$$ ||\hat{q}||=\sqrt{\hat{q}^*\hat{q}} =||q_0||+\frac{\varepsilon (q_0\cdot q_\varepsilon) }{||q_0||} $$

P58

Dual Quaternion

• Unit dual quaternion: \(||\hat{q}||=1\), which requires:

$$ ||q_0||=1 $$

$$ q_0 \cdot q_\varepsilon=0 $$

P59

Dual Quaternion ⇔ Rigid Transformation

• Like quaternion, any rigid transformation \(T \in SE(3)\) can be converted into a unit dual quaternion

$$ Tx=Rx+t $$

$$ T=[R\mid t]\to \hat{q} =q_0+\varepsilon q_\varepsilon $$

$$ \begin{matrix} q_0=r \quad & \text{ quaternion of } R \quad \quad\quad\quad\\ q_\varepsilon =\frac{1}{2} tr & \text{ pure quaternion } t = (0,t) \end{matrix} $$

✅ 把一个刚性变换表示为对偶四元数。

P60

Dual Quaternion ⇔ Rigid Transformation

• Transform a vector \(v\) using unit dual quaternion

$$ {\hat{v} }' =\hat{q} \hat{v} \hat{q} ^\star $$

where

$$ \begin{align*} \hat{v} & = 1+\varepsilon (0,v) \\ & =(1,0,0,0)+\varepsilon (0,v_x,v_y,v_z) \end{align*} $$

$$ \quad $$

$$ \mathrm{III}: \hat{q} ^ \star = q ^ * _ 0 - \varepsilon q ^ *_ \varepsilon $$

$$ \quad \quad \quad \quad = ({\hat{q} ^ *}) ^ {\circ} = (\hat{q} ^ {\circ}) ^ * $$

P61

Dual Quaternion ⇔ Rigid Transformation

• Like quaternion, any rigid transformation \(T \in SE(3)\) can be converted into a unit dual quaternion

$$ T=[R\mid t]\to \hat{q} =q_0+\varepsilon q_\varepsilon $$

$$ \begin{matrix} q_0=r \quad \\ q_\varepsilon =\frac{1}{2} tr \end{matrix} $$

\(\hat{q}\) and \(-\hat{q}\) represent the same transformation \(\hat{Q}\) is a double cover of \(SE(3)\)

P62

Double Cover Visualized

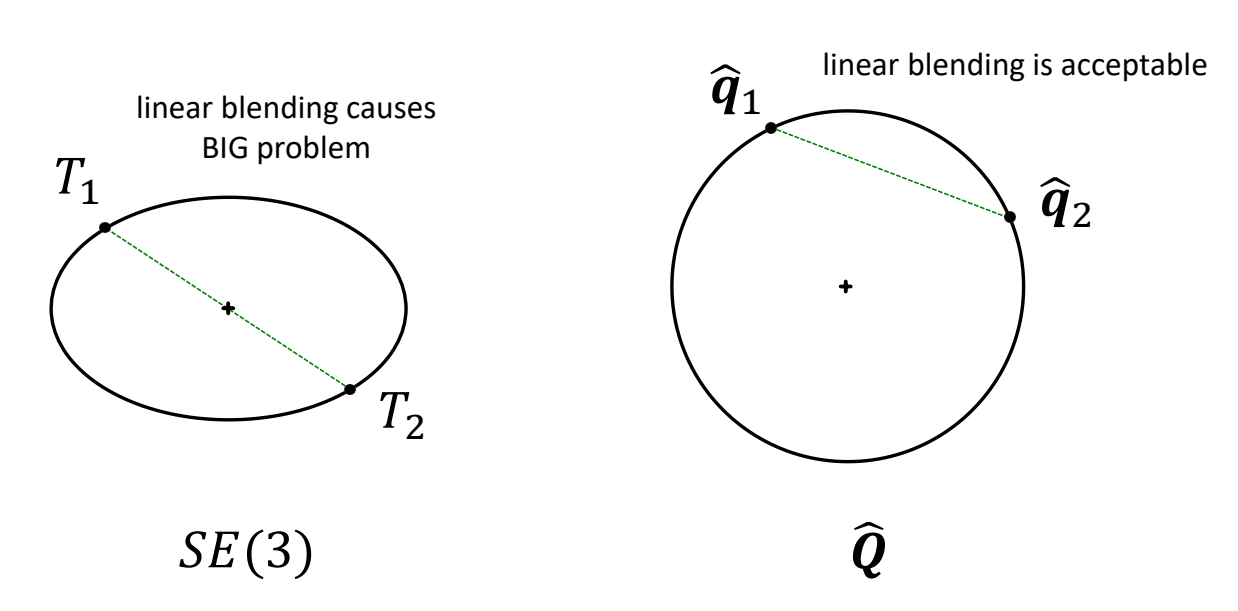
P63

Interpolating Dual-Quaternion

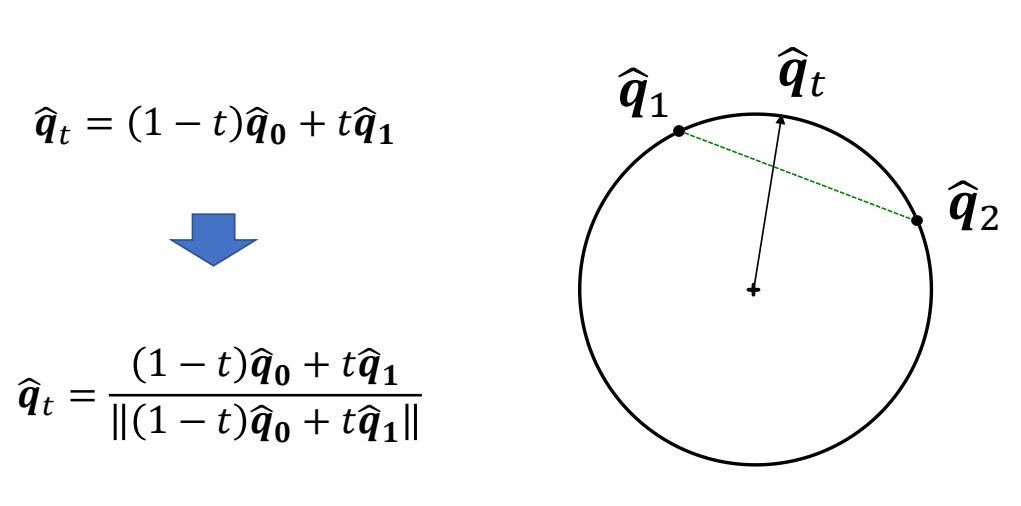
P64

Dual-Quaternion Linear Blending (DLB)

P65

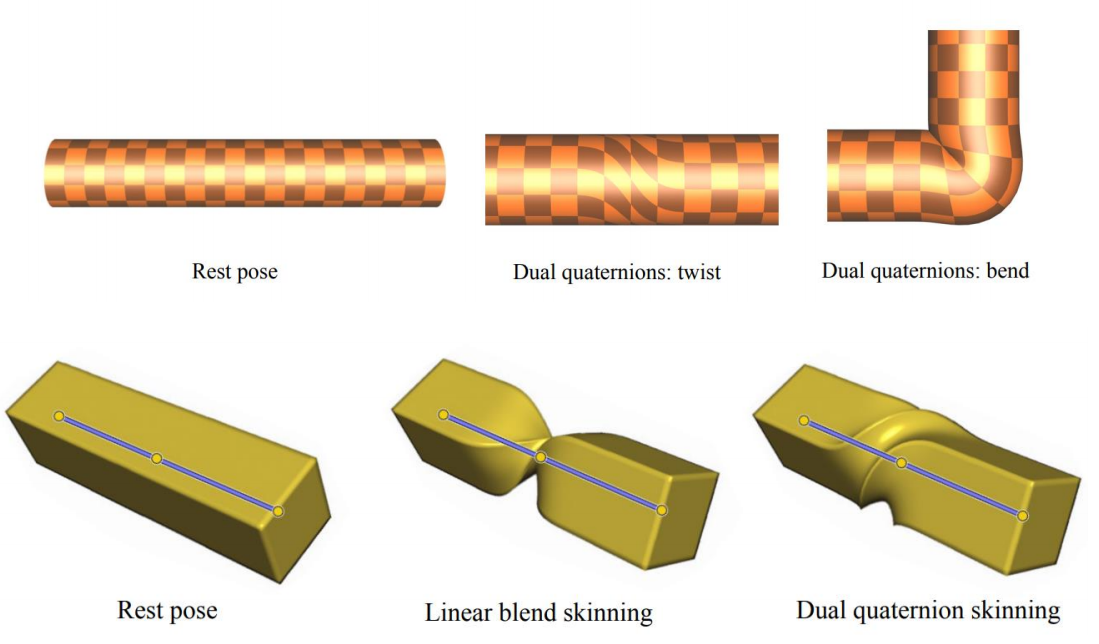
Dual-Quaternion Skinning (DQS)

P66

Budging Artifact of DQS

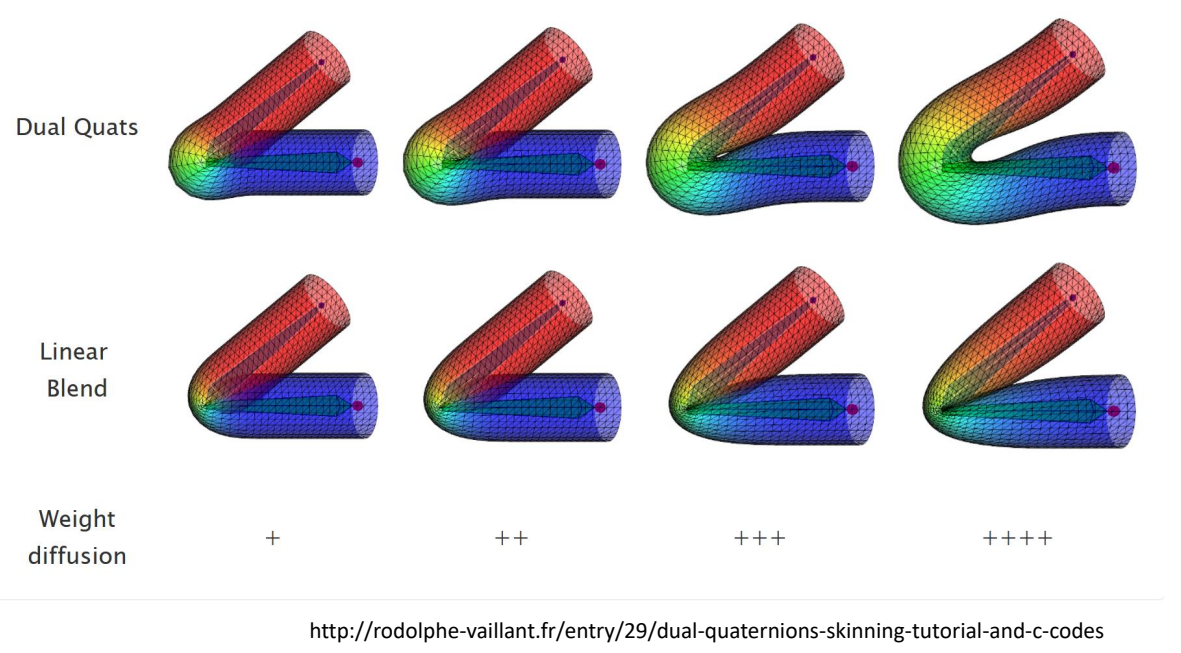
✅ 越往右蒙皮权重越光滑。
✅ DQBS 也有比较严重的 artifacts.

P67

How to Correct LBS?

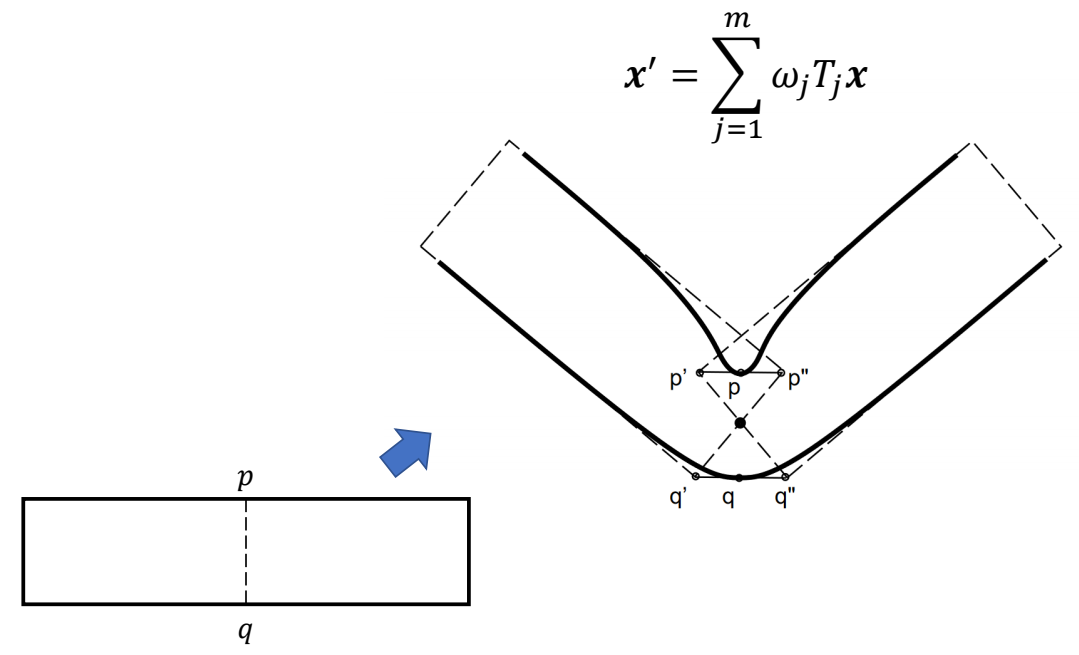
✅ LBS 的天然缺陷

P69

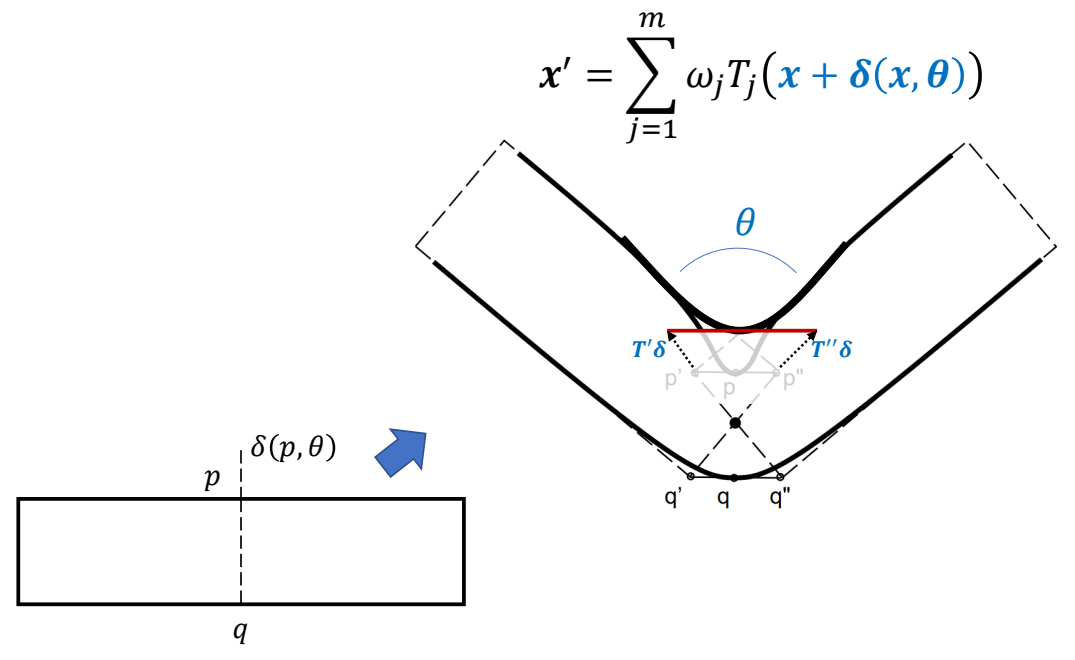
How to Correct LBS?

P74

Scattered Data Interpolation

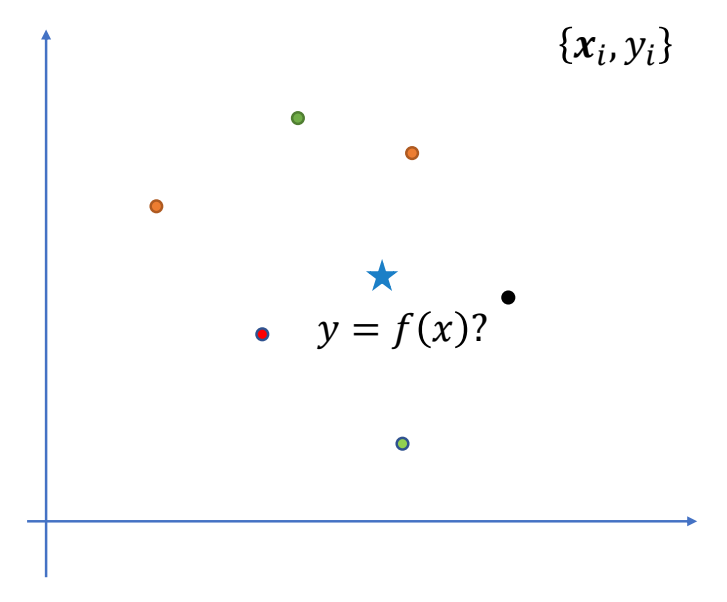
P76

Scattered Data Interpolation

• Linear
  • Least squares
• Splines
• Inverse distance weighting
• Gaussian process
• Radial Basis Function
• ……

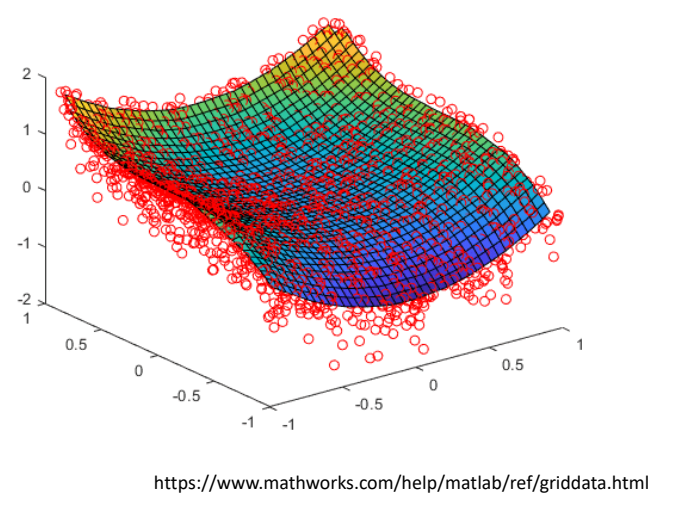
P81

Radial Basis Function (RBF) Interpolation

$$ y=\sum_{i=1}^{k} w_i\varphi (||x-x_i||) $$

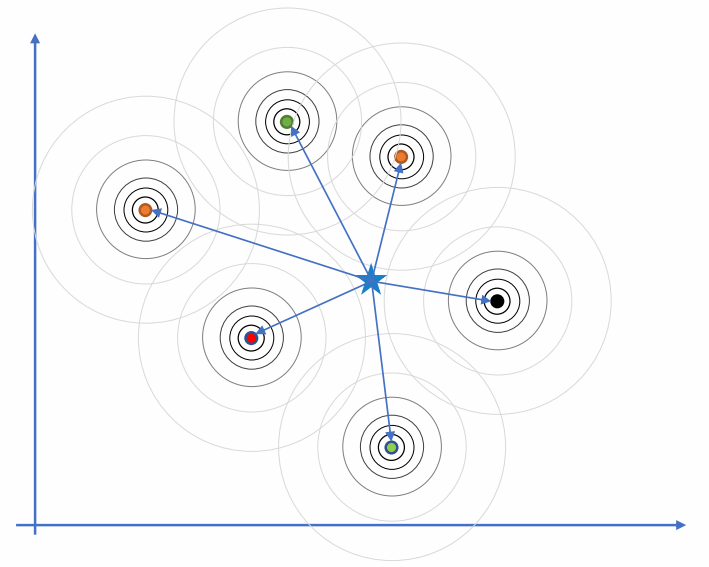
P83

Radial Basis Function (RBF) Interpolation

$$ y=\sum_{i=1}^{k} w_i\varphi (||x-x_i||) $$

How to compute \(w_i\) ? We need \(f(x_i)=y_i\)

$$ \begin{bmatrix}
R_{1,1} & R_{1,2} & \cdots & R_{1,K} \\
R_{2,1} & R_{2,2} & & \vdots \\
\vdots & & \ddots & \vdots \\
R_{K,1} & \cdots & \cdots & R_{K,K}
\end{bmatrix} \begin{bmatrix} w_1\\ w_2 \\ \vdots\\ w_K \end{bmatrix}=\begin{bmatrix} y_1\\ y_2 \\ \vdots\\ y_K \end{bmatrix} $$

$$ R_{i,j}=\varphi (||x_i-x_j||) $$

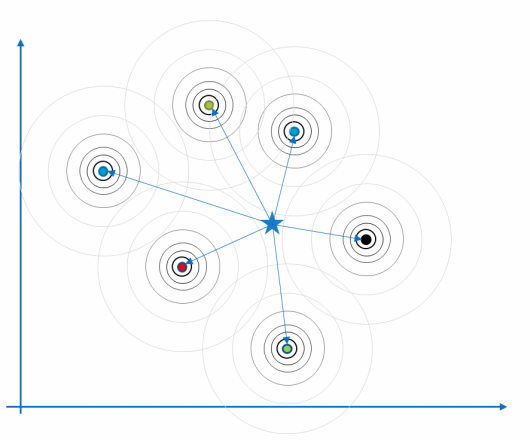
P84

Radial Basis Function (RBF)

$$ y=\sum_{i=1}^{k} w_i\varphi (||x-x_i||) $$

• Gaussian:

$$ \varphi (r)=e^{-(r/c)^2} $$

• Inverse multiquadric:

$$ \varphi (r)=\frac{1}{\sqrt{r^2+c^2} } $$

• Thin plate spline:

$$
\varphi (r)=r^2 \log r $$

• Polyharmonic splines:

$$ \varphi (r)=\begin{cases} r^k,k=2n+1\\ \\
r^k \log r,k=2n \end{cases} $$

P85

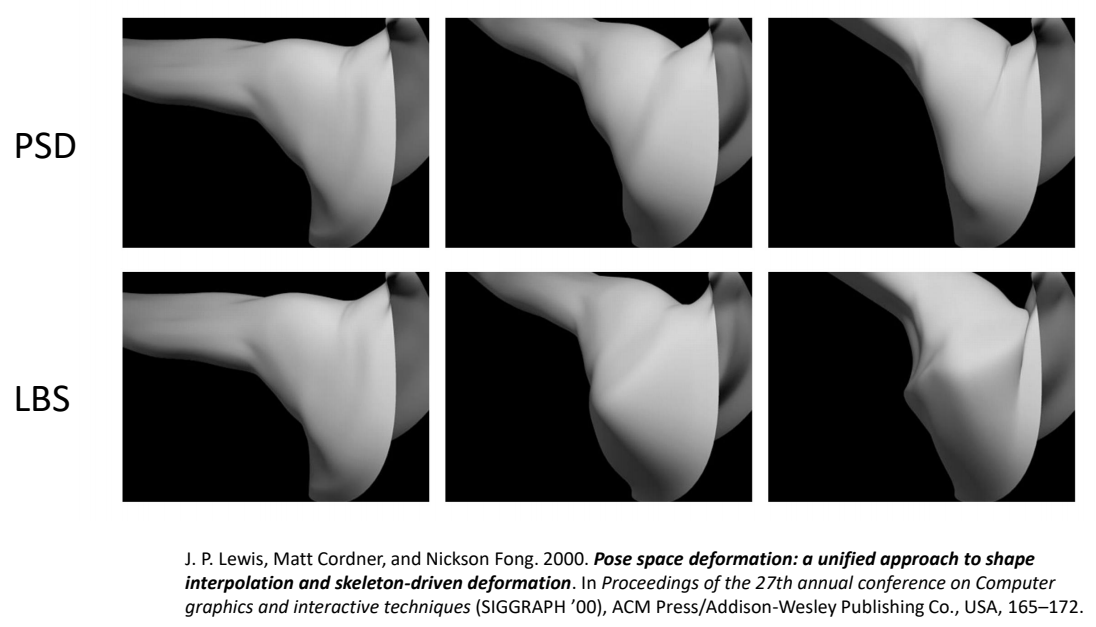
Pose Space Deformation

$$ {x}' =\sum_{j=1}^{m} w_iT_j (x+\delta (x,\theta )) $$

• \({x}'= SKIN(PSD(x))\)
• 𝑃𝑆𝐷 is implemented as RBF interpolation
• Example shapes can be created manually
  • Or by 3D scanning real people → the SMPL model

J. P. Lewis, Matt Cordner, and Nickson Fong. 2000. Pose space deformation: a unified approach to shape

interpolation and skeleton-driven deformation. In Proceedings of the 27th annual conference on Computer

graphics and interactive techniques (SIGGRAPH ’00), ACM Press/Addison-Wesley Publishing Co., USA, 165–172.

P86

Pose Space Deformation

P87

Issues

• Per-shape or per-vertex interpolation
  • Should we interpolate a shape as a whole?
• Local or global interpolation?
  • Should a vertex be affected by all joints?
• Interpolation algorithm?
  • Is RBF the only choice?

SIGGRAPH Course 2014 — Skinning: Real-time Shape Deformation

P88

Example-based Skinning (EBS) vs. Skeleton Subspace Deformation (SSD)

\(^\ast \)EBS: PSD
\(\quad\)

• Good: Easy to control
• Good: Good quality
• Good: Pose-dependent details (e.g. bulging muscle and extruding veins)

\(\quad\)

• Bad: Creating examples can be cumbersome
• Bad: Extra storage for examples
• Bad: Interpolation needs careful tuning

\(\quad\)

\(^\ast \)SSD: LBS, DQS, etc.
\(\quad\)

• Good: Easy to implement
• Good: Fast and GPU friendly

\(\quad\)

• Bad: Various artifacts
• Bad: Skinning weights needs careful tuning
• Bad: Hard to create pose-dependent details

P89

Example: SMPL Model

• A widely adopted human model in ML/CV
• Learned on real scan data
• Combines SSD and EBS techniques

P92

Recall: Principal Component Analysis (PCA)

• Given a dataset {\(x_i\)}, \(x_i \in \mathbb{R} ^N\), then PCA gives

$$ x_i=\bar{x}+\sum_{k=1}^{n} w_{i,k}u_k $$

• \(u_k\) is the \(k\)-th principal component
  • A direction in \( \mathbb{R} ^N\) along which the rojection of {\(x_i\)} has the \(k\)-th maximal variance
• \(w_{i,k}=(x_i-\bar{x})\cdot u_k\) is the score of \(x_i\) on \(u_k\)

P93

Recall: Principal Component Analysis (PCA)

• Given a dataset {\(x_i\)}, \(x_i \in \mathbb{R} ^N\), the PCA can be computed by apply eigen decomposition on the covariance matrix

$$ \sum =X^TX=U\begin{bmatrix} \sigma ^2_1 & & & \\ & \sigma ^2_2 & & \\ & & \ddots & \\ & & \sigma ^2_N \end{bmatrix}U^T $$

• \(X=[x_0-\bar{x}, x_1-\bar{x},\dots ,x_N-\bar{x}]^T\)

• \(\sigma _i\ge \sigma _j\ge 0\) when \(i< j\), corresponds to the Explained Variance

• \(U=[u_1,u_2,\dots,u_N]\)

P94

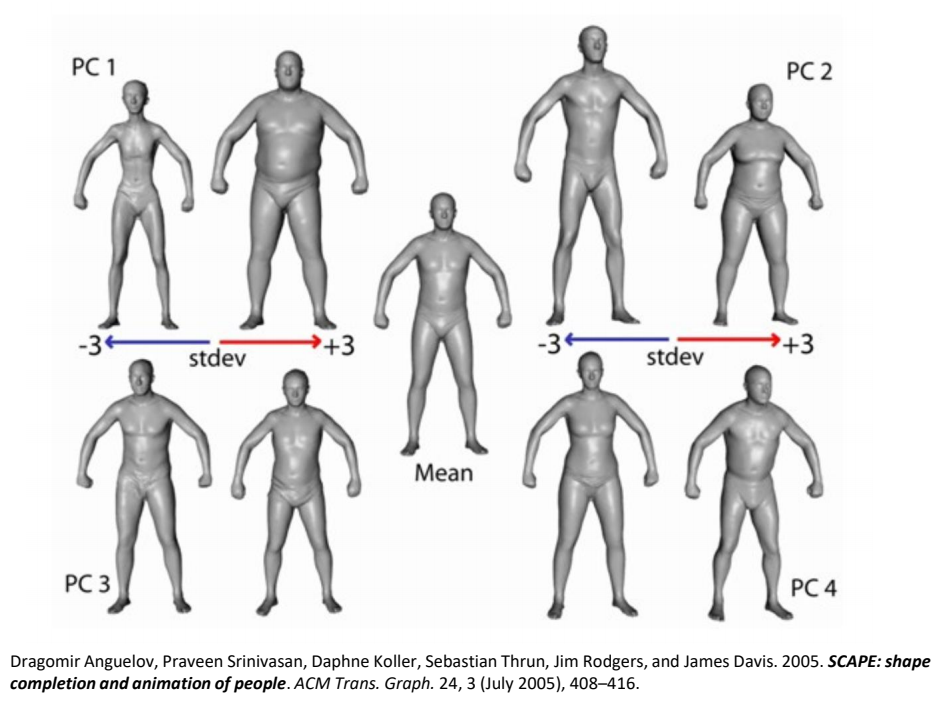
PCA over Body Shapes

P95

SMPL Model: Body Shape

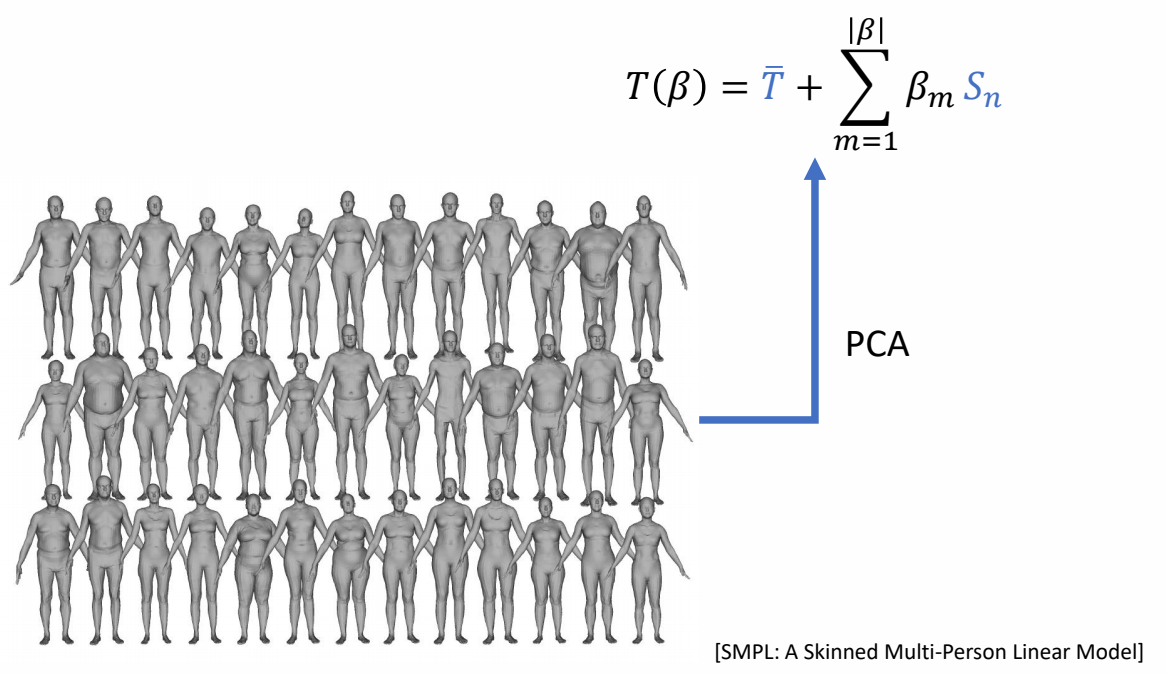
P96

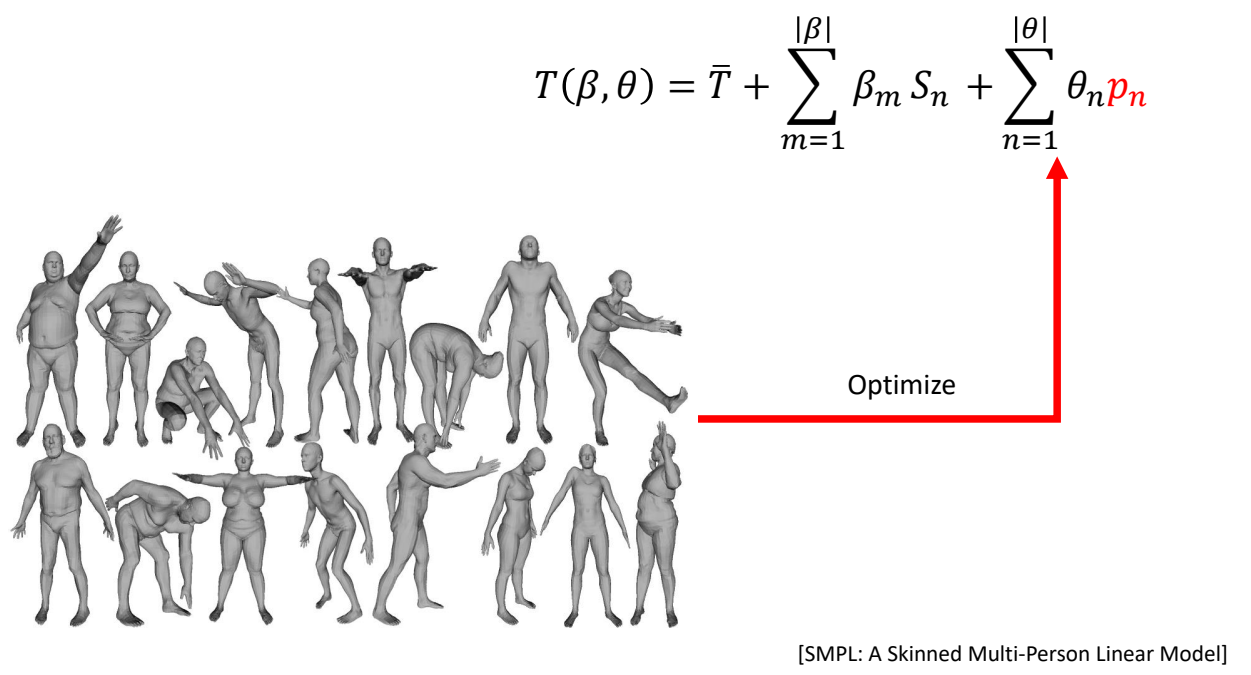
SMPL Model: Pose Blend Shapes

P97

SMPL Model: Deformation

$$ T(\beta ,\theta )=\bar{T} + \sum _ {m=1}^{|\beta |} \beta _ m S_ n + \sum _ {n=1}^{|\theta |}\theta _np_n $$

$$ x=SKIN(T(\beta ,\theta ),\theta ,w) $$

$$ SKIN:\text{LBS, DQS, etc}\dots $$

[SMPL: A Skinned Multi-Person Linear Model]

P99

Facial Animation

P101

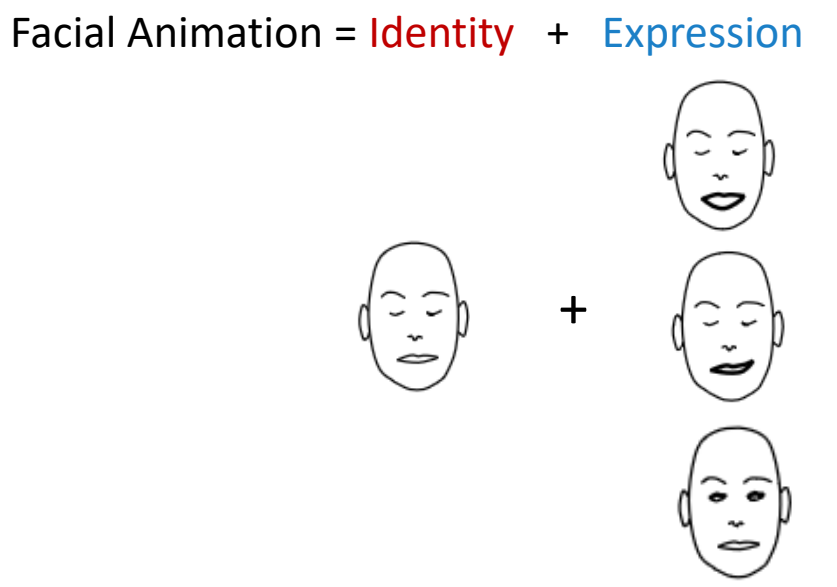
Facial Animation

✅ \(B_j\) 与 ID 无关，能做出差不多的效果。
✅ 要更精细的效果，可以定义与 ID 相关的 \(B_j\).

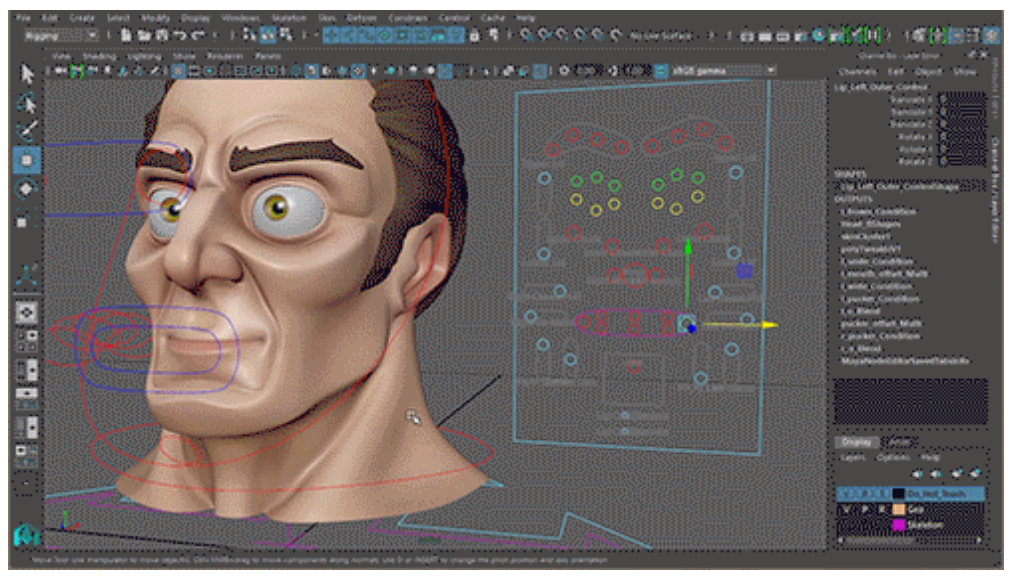
P102

Facial Blendshapes

P103

A Typical Set of Blendshapes (ARKit)

P104

Blendshapes vs. Example-based Skinning

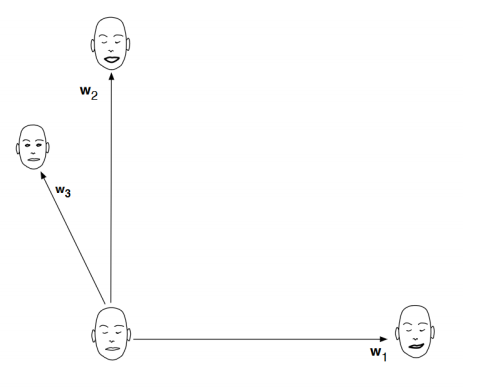
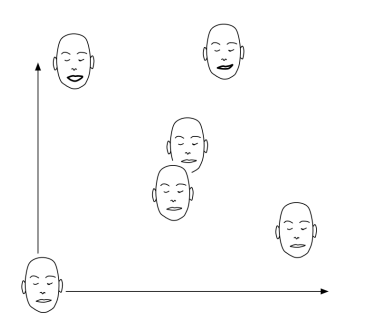
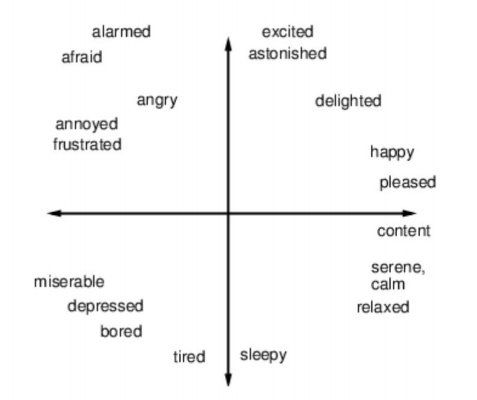
✅ 几种不同的表情基混合方式。
✅ 第二种，直接在几个脸之间做混合，适用于数据少的情况。

P105

Morphable Face Models

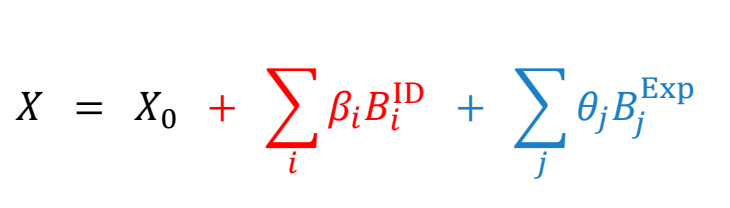
Egger et al. 2020. 3D Morphable Face Models - Past, Present, and Future. ACM Trans. Graph. 39, 5 (June 2020), 157:1-157:38.

✅ 第一项：平均脸。第二项：PCA. 第三项：表情基。
✅ \(B_i^{ID}\) 通常由 PCA 得到。
✅ 基于脸部肌肉的物理仿真。

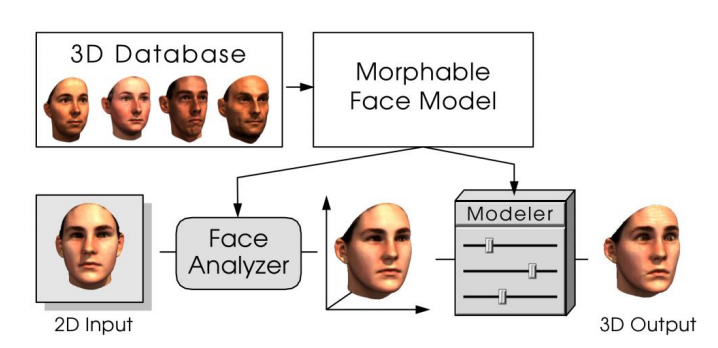
P107

How to Animate a Face?

P110

Face Tracking

✅ 用一个视频人脸驱动 3D 人脸。
✅ 人脸 \(\overset{①}{\rightarrow} \) 特征点 \(\overset{②}{\rightarrow} \) 表情参数
✅ 1、提取 \(\quad\) 2、IK．

ReadPapers 蒙皮绑定相关论文索引

以下论文收录于 ReadPapers 项目，按核心程度分组。

核心蒙皮 / 绑定论文

基于 LBS 扩展的新表示方法

动物/人脸绑定

说明：论文 ID 对应 ReadPapers 项目中的编号，点击可跳转至完整笔记。其中 235 (SSDR) 和 236 (Rigging) 是本节内容的直接延伸阅读；220 (GaussiAnimate) 展示了经典 LBS/DQS 思想在 3DGS 新表示中的延续。

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES105_mdbook/