P4

Recap

Dynamics of a Point Mass

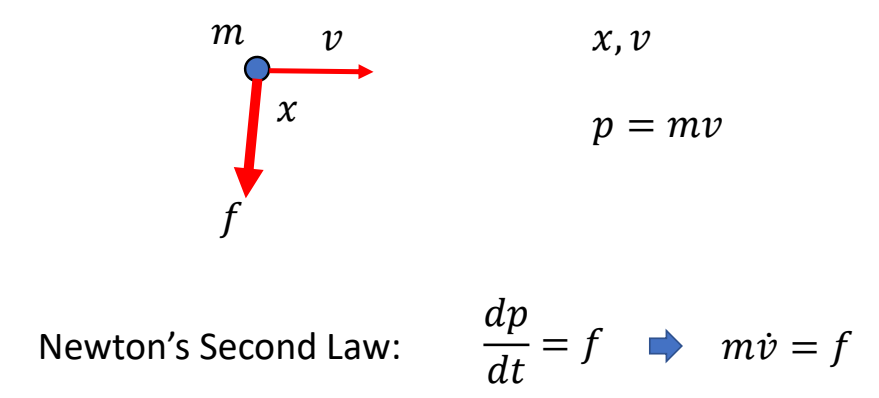
P10

Rigid Body Dynamics

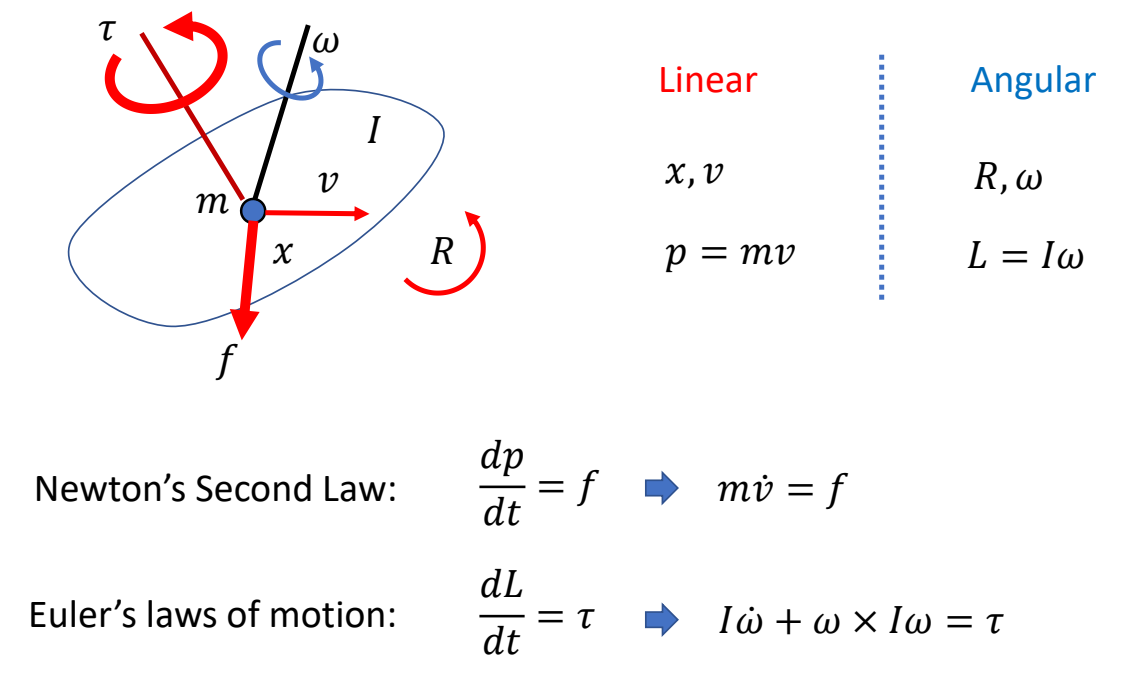
$$ \begin{bmatrix} mI_3 & 0\\ 0 & I \end{bmatrix}\begin{bmatrix} \dot{v} \\ \dot{\omega } \end{bmatrix}+\begin{bmatrix} 0\\ \omega \times I\omega \end{bmatrix}=\begin{bmatrix} f \\ \tau \end{bmatrix} $$

P12

Masses: \(m,I\)
Kinematics: \(x,v,R,\omega \)

Geometry:
• Box, Sphere, Capsule, Mesh, …
• Collision detection
• Compute \(m,I\)

✅ 在物理引擎里面定义一个刚体，需要提供这些参数。

P14

Dynamics of Articulated Rigid Bodies

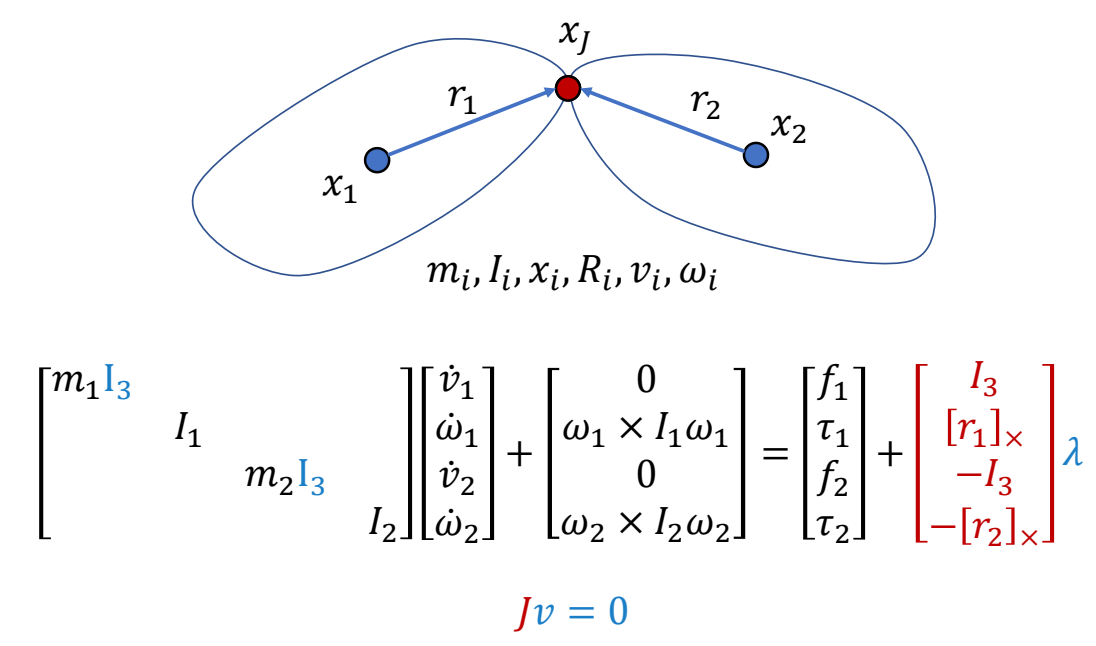
✅ 两个独立刚体，和一个不让它们断开的约束。

P15

$$ M\dot{v} +C(x,v) =f+J^T\lambda $$

P16

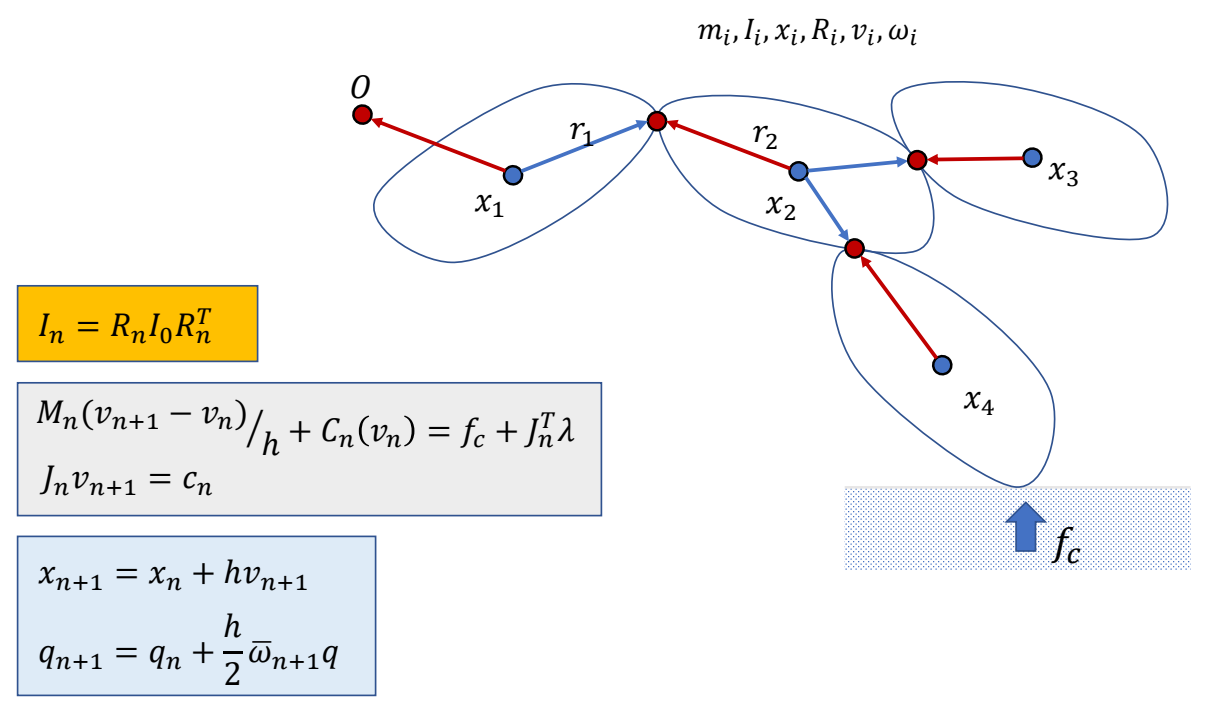
Simulation of a Rigid Body System

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES105_mdbook/