✅ 基于数据：对现有数据进行连接重组。
✅ 基于学习：对数据处理，放入模型，再生成数据。

Outline

Recap: interactive character animation
- Motion Graphs
- Motion Matching
Statistical Models of Human Motion
- Principal Component Analysis
- Gaussian Models

Recap: Interactive Animation

How to make a character respond to user command?

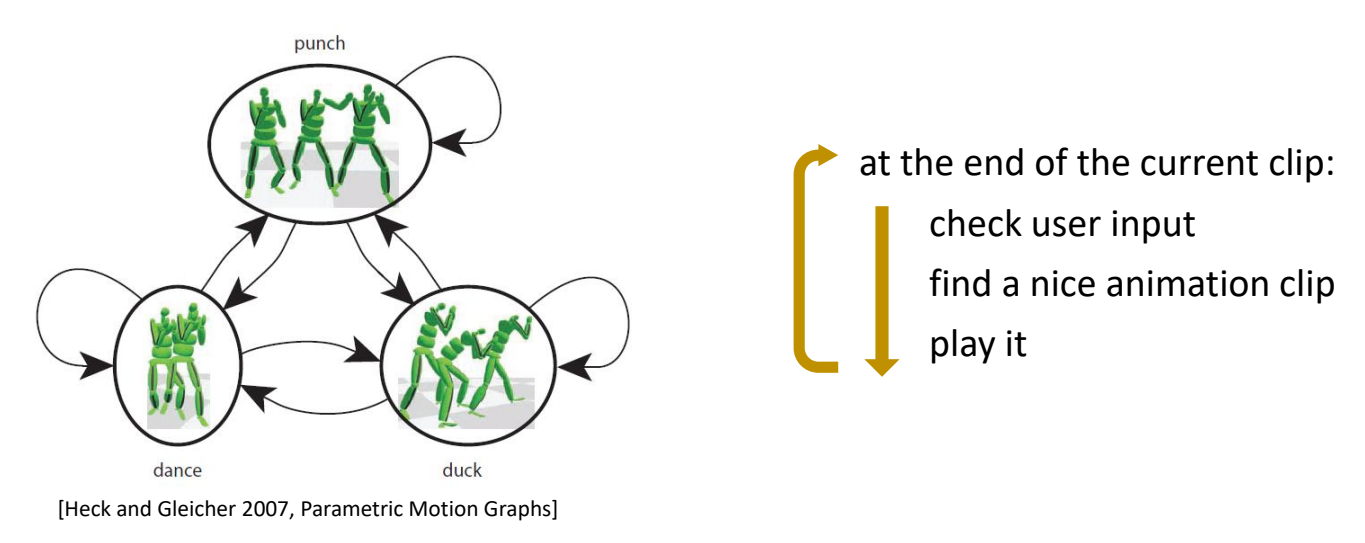
Motion Graphs

✅ 检测到用户输入后：

把当前片段播完（响应慢）

所有下一片断与当前状态进行坐标系对齐

根据当前状态和预期轨迹，选择下一个片断

播放对齐后的下一片断

✅ 可以结合路径规划算，实现一些智能角色。Motion Graph 只是一个底层数据结构。

P14

Motion Fields


Motion Graphs / State Machines	Motion Fields / Motion Matching

✅ Motion Matching 是将 Motion Fields 简化以后加一些比较好的工程实践。

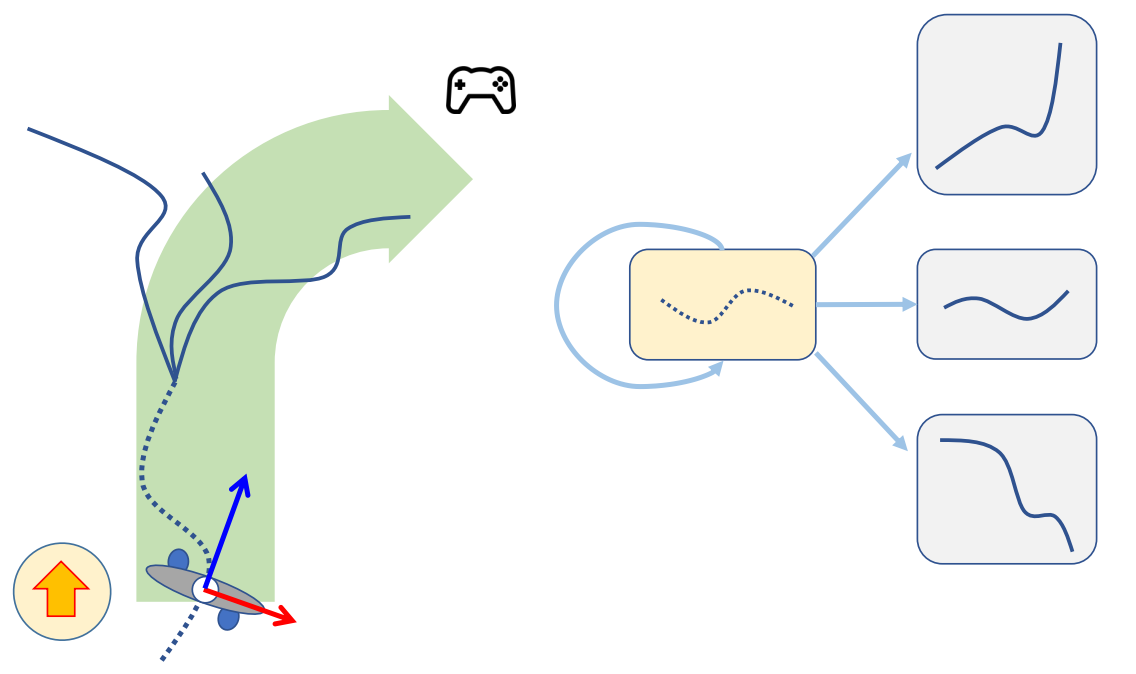
P17

构建 Motion Fields

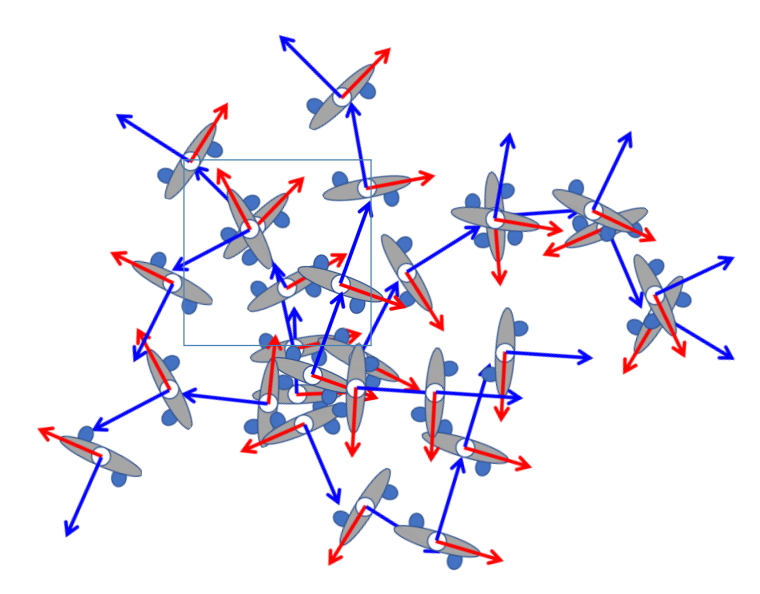
✅ 每条链路代表一个动作，灰圈代表动作里的一帧，整体构成一个很大的 Field.

P20

在Motion Fields中选择pose

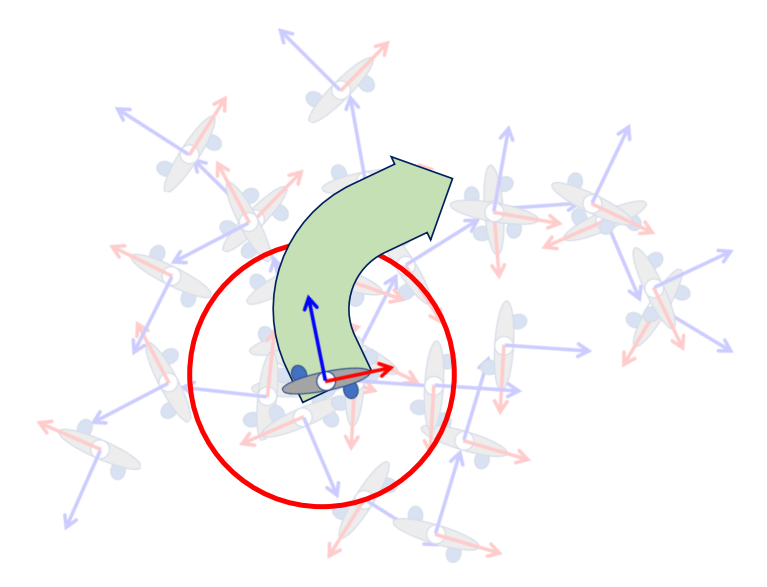
✅ 每一帧有一些最近邻，它们来自不同动作，有不同的状态。
✅ 绿色代表向右，挑出对应帧。做混合。

P23

对pose的混合

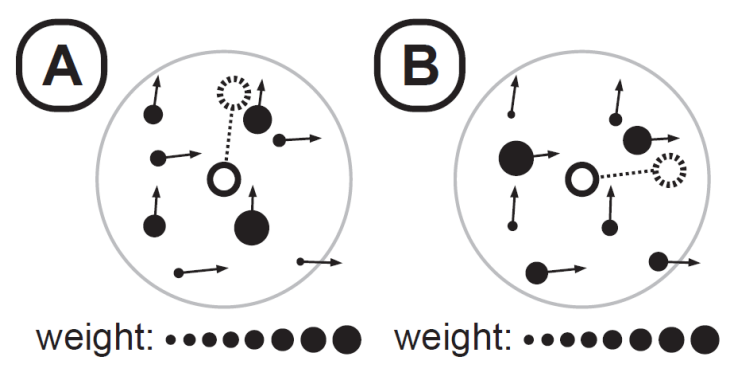
✅ 根据用户输入设置不同权重，会得到不同结果
✅ 优点：(1) 自由控制（2）支持外力，可结果物理仿真（3）不需要使首尾帧相似的预处理。
✅ 缺点：需要设计一些规则来计算最近邻的混合。
✅ 解决方法：强化学习

P24

Pipeline

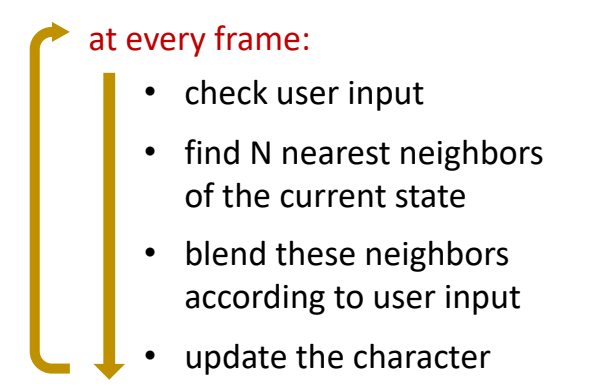
✅ 根据用户输入设计邻局的权重，这一步难以工业化。
✅ 论文使用强化学习来解决，这样增加了训练的难度。

P31

Motion Matching

P32

✅ 简化一：只找一个最近邻，不需要 blend. 然后用平滑解决跳变问题。

P34

距离衡量函数

We need a distance function / metric to define the nearest neighbor

$$ \text{next-pose } = \min_{i \in\text{ Dataset}} ||x_{\text{curr}}-x_i|| $$

$$ x: \text{feature vector} $$

✅ Motion Matching 中距离函数的设计很重要，很大程度上影响算法的效果。
✅ 这个距离定义可以是特征相关的。

A possible set of feature vectors:

root linear/angular velocity
position of end effectors w.r.t. root joint
linear/angular velocity of end effectors w.r.t. root joint
future heading position/orientation (e.g. in 0.5s, 1.0s, 1.5s, etc.)
foot contacts
……

P36

动作平滑

We need a smooth motion

Only do the search every few frames
Smoothly blend current pose to the target pose
- Inertialized blending (ref. https://www.theorangeduck.com/page/spring-roll-call by Daniel Holden)

搜索效率

We need a good performance

An efficient data structure for searching，例如 e.g. KD-tree

数据集

A efficient dataset，例如“Dance card”

✅ 保证所使用的动作集能够覆盖到目标。
✅ 优点：(1) 实现简单 (2) 控制灵活 (3) 可结合物理仿真。
✅ 缺点：(1) 不能解决滑步

P39

Statistical Models of Human Motion

✅ 根据已有数据，对“动作自然”建模。
✅ 或找到一个模型，告诉我们什么是自然姿态。

P43
因为由于以下原因， “自然的动作”实际上是够成高维的动作参数空间的流形曲面。

Coordinated arm/leg movement
Musculoskeletal structure
Laws of physics
……

P45

Principal Component Analysis (PCA)

A technique for
- finding out the correlations among dimensions
- dimensionality reduction

✅ PCA 细节跳过。目的：降维，抓住主要特征。

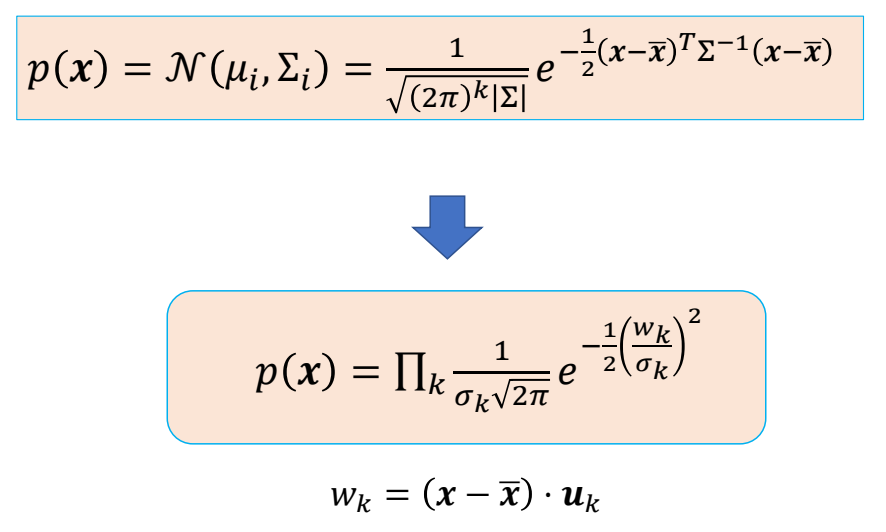
P65

a pose $x$ with smaller $\sum _k\frac{((x-\bar{x})\cdot u_k)^2 }{\sigma ^2_k}$ is more likely to be a good pose

✅ 可作为动作生成的先验，告诉我一个动作是否合理。
✅ $M_k$ 和 $\sigma_k$ 分别是 $k$ 维上的均值和方差。

P66

Character IK with a Motion Prior

正则化先验

$$ F(\theta )=\frac{1}{2} \sum_{i}^{} ||f_i(\theta )-\tilde{x} _i||^2_2+\frac{\lambda }{2}||\theta ||^2_2 $$

$$ \theta=(t_0,R_0,R_1,R_2\dots \dots ) $$

✅ 正则项代表主观先验: $\theta $ 小更有可能是合理动作。

P68

PCA先验

$$ F(\theta )=\frac{1}{2} \sum_{i}^{} ||f_i(\theta )-\tilde{x} _i||^2_2 $$

$$ +\frac{w }{2}\sum_{k}^{}(\frac{(\theta -\bar{\theta })\cdot u_k }{\sigma _k} )^2 $$

✅ 把 P65 方法应用到 IK 来判断动作好坏的实例。
✅ 改进为基于统计的先验。

P71

Data Distribution

$p(x)$ : probability that $x$ is a natural pose

✅ 假设存在这样一个分布，但不知道分布的具体形式，要估计这样的分布
✅（1）从分布中采样，例如：动捕
✅（2）通过各种模型把分布估计出来，即从数据中估计出模型参数。

P75

Gaussian Distribution

✅ 假设分布就是高斯分布

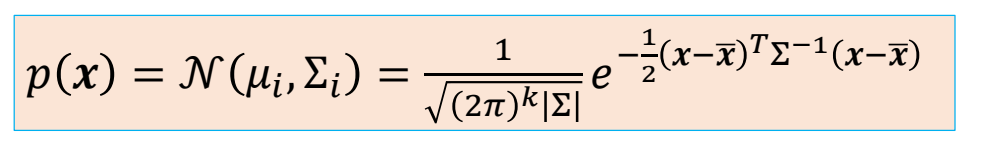
通过Maximum Likelihood Estimators (MLE，最大似然估计)得到:

$$ \begin{align*} \bar{x} &= \frac{1}{N} \sum_{i}^{} x_i \\ \Sigma & =\frac{1}{N} X^TX \end{align*} $$

P76

PCA 可以看作一种高斯分布。

$$ \sum =X^TX=U\begin{bmatrix} \sigma ^2_1 & & & \\ & \sigma ^2_2 & & \\ & & \ddots & \\ & & &\sigma ^2_N \end{bmatrix}U^T $$

$$ x-\bar{x} =\sum_{k=1}^{n} w_ku_k $$

✅ PCA 分解可以看作是坐标转换或变量代换。

P77

P78

Character IK with a Motion Prior

$$ F(\theta )=\frac{1}{2} \sum_{i} ||f_i(\theta )-\tilde{x} _i||^2_2+\frac{w}{2}\sum_k(\frac{(\theta -\bar{\theta })\cdot u_k }{\sigma _k} )^2 $$

P79

$$ F(\theta )=\frac{1}{2} \sum_{i}^{} ||f_i(\theta )-\tilde{x} _i||^2_2-w \log \prod_k e^{-\frac{1}{2}(\frac{(\theta -\bar{\theta })\cdot u_k }{\sigma _k} )^2 } $$

P80

$$ F(\theta )=\frac{1}{2} \sum_{i}^{} ||f_i(\theta )-\tilde{x} _i||^2_2-w \log p(\theta )
$$

$$ \theta=(t_0,R_0,R_1,R_2\dots \dots ) $$

✅ 第一项：符合目标。第二项：动作合理。

P81

Motion Synthesis with a Motion Prior

Given a motion prior $p(x)$ learned from a set of data points $D $= {$x_i$}, Synthesize a motion $x$ that minimize the objective

$$ f(x)=f(x)-w \log p(x ) $$

Note: $x$ can represent a pose $\theta$
$\quad\quad$ or a motion clip → a sequence of poses {$ \theta t$}
$\quad\quad$ or any features of a motion → e.g. $w_k$ in PCA

✅ $x$ 可以不局限于 $\theta $、而是任何一个可以描述 motion 的量。
✅ $f(x)$ 代表目标，目标也不局限于 IK，也可以是Keyframes、User control、Environment constraints等
✅ 但“认为动作符合高斯分布”仍然是一个非常受限约束，难以用于复杂的动作

P83



	✅ 使用高斯混合模型，用于动作编辑。 ✅ \(x\) 不局限于单帧动作，也可以是一个序列。
Min et al. 2009	✅ 视频动捕是欠约束问题，但可以通过分布过滤掉不合理的结果。
	✅ 缺点：实现麻烦，很多超参。
	[Starke et al 2020, Local Motion Phases for Learning Multi-Contact Character Movements]
	[Henter et al. 2020, MoGlow: Probabilistic and Controllable Motion Synthesis Using Normalising Flows] ✅ 利用 RL 等方法，在 lalent code 上生成轨迹，再把轨迹转到动作空间。
	[Lee et al 2019, Interactive Character Animation by Learning Multi-Objective Control]
	[Holden et al 2020, Learned Motion Matching] ✅ 用 DL 代替复杂的模型，来估计动作先验。

GAMES105

Outline

Recap: Interactive Animation

Motion Graphs

Motion Fields

构建 Motion Fields

在Motion Fields中选择pose

对pose的混合

Pipeline

Motion Matching

距离衡量函数

动作平滑

搜索效率

数据集

Statistical Models of Human Motion

Principal Component Analysis (PCA)

Character IK with a Motion Prior

正则化先验

PCA先验

Data Distribution

Gaussian Distribution

PCA 可以看作一种高斯分布。

Character IK with a Motion Prior

Motion Synthesis with a Motion Prior

相关工作