P4

Physics-based Character Animation

[ControlVAE – Yao et al. 2022]

角色的运动方式依赖于力学而不是数据。

✅ 物理方法的难点：
✅ (1) 仿真：在计算机中模拟出真实世界的运行方式。
✅ (2) 控制：生成角色的动作，来做出响应。

P5

Outline

• Simulation Basis
  • Numerical Integration: Euler methods
• Equations of Rigid Bodies
  • Rigid Body Kinematics
  • Newton-Euler equations
• Articulated Rigid Bodies
  • Joints and constraints
• Contact Models
  • Penalty-based contact
  • Constraint-based contact

https://www.cs.cmu.edu/~baraff/sigcourse/

✅ 角色物理动画通常不关心仿真怎么实现。
✅ 但也可以把仿真当成白盒，用模型的方法来实现。

P57

Kinematics vs. Dynamics

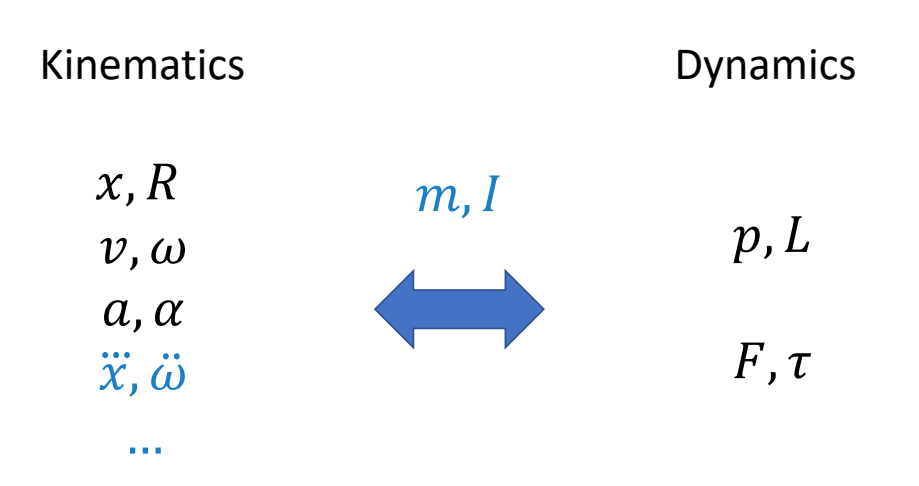
✅ 运动学与动力学，主要区别在于有没有考虑角色质量。因为质量代表惯性，有惯性就不能瞬移。
✅ 动力学基本概念跳过。P58-P89

本文出自CaterpillarStudyGroup，转载请注明出处。

https://caterpillarstudygroup.github.io/GAMES105_mdbook/