P2
Outline
-
Walking and Dynamic Balance
-
Simplified Models
- ZMP (Zero-Moment Point)
- Inverted Pendulum
- SIMBICON
✅ 不能直接控制角色位置,而是通过与地面的力和反作用力。
P3
Walking
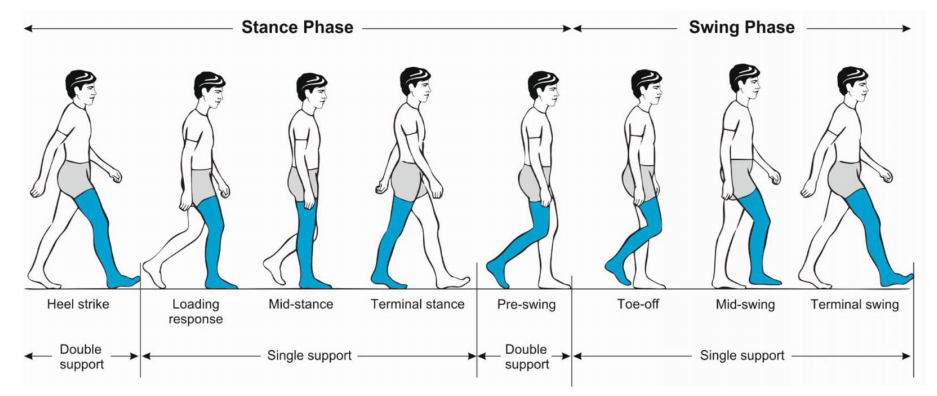
🔎 Gait disorders in adults and the elderly.
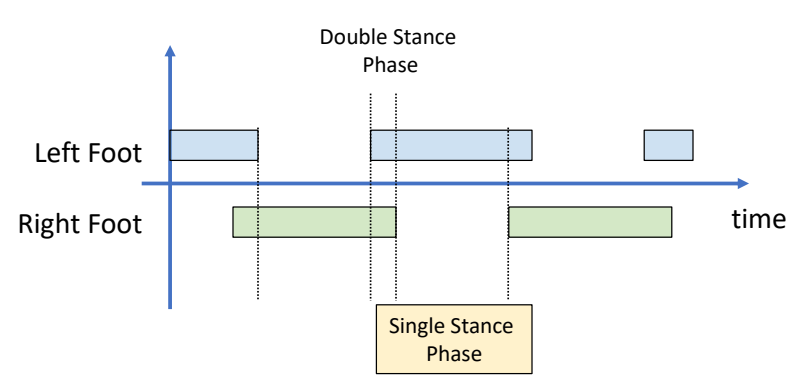
phases of a walking gait cycle
Pirker and Katzenschlager 2017.
P4
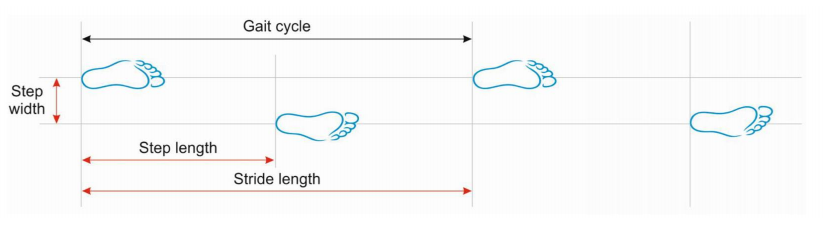
Walking VS Running
| Walking | Running |
|---|---|
 Walking: move without loss of contact, or flight phases | 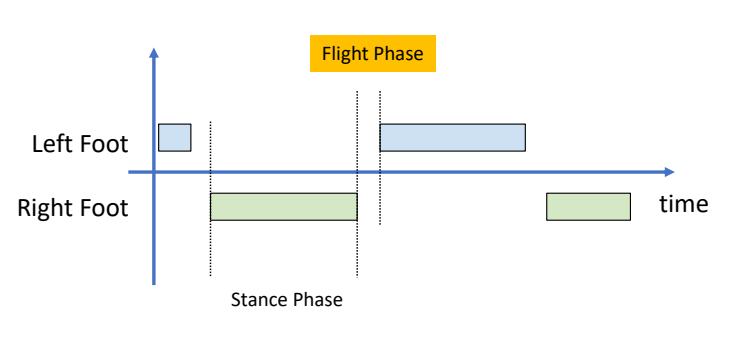 |
P7
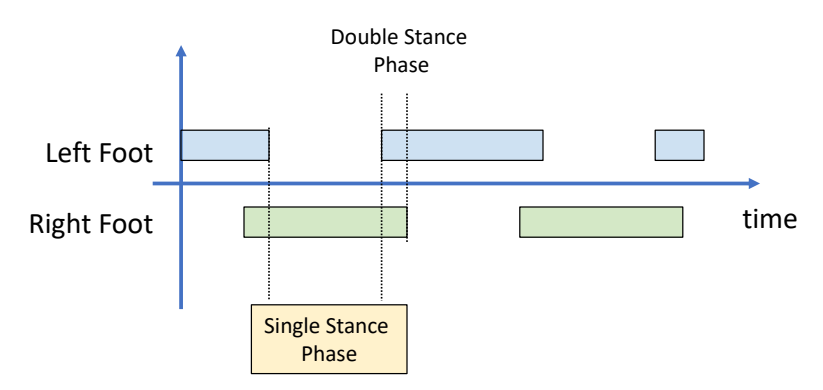
Walking的几个阶段
 | 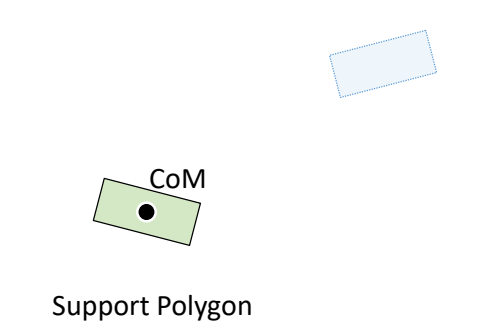 |
 | 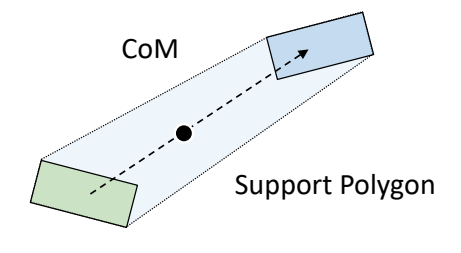 |
 | 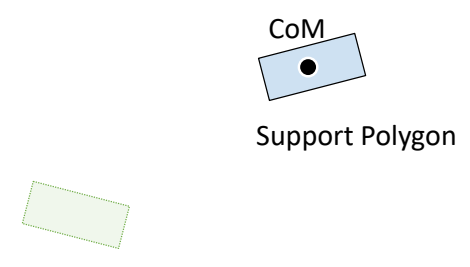 |
✅ 以上过程假设角色处于 static 状态。没有考虑到移动过程中的脚的动量。因此只能勉强保持角色稳定。要以非常慢的速度相前移动。
本文出自CaterpillarStudyGroup,转载请注明出处。
https://caterpillarstudygroup.github.io/GAMES105_mdbook/